2015-2016学年广东省深圳市南山区八年级上学期期末数学试卷（1）

试卷更新日期：2016-12-30 类型：期末考试

进入出卷网下载

一、选择题

1. 下列实数中，无理数是（）

A、﹣1 B、 $\frac{1}{2}$ C、3. $\dot{1} \dot{4}$ D、 $\sqrt{3}$

查看试题解析
2. 函数y= $\frac{\sqrt{x + 3}}{x - 5}$ 中自变量x的取值范围是（）

A、x≥﹣3 B、x≠5 C、x≥﹣3或x≠5 D、x≥﹣3且x≠5

查看试题解析
3. 如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD= $\sqrt{5}$ ，则BC的长为（）

A、 $\sqrt{3}$ ﹣1 B、 $\sqrt{3}$ +1 C、 $\sqrt{5}$ ﹣1 D、 $\sqrt{5}$ +1

查看试题解析
4. 下列计算正确的是（）

A、x⁷÷x⁴=x¹¹ B、（a³）²=a⁵ C、2 $\sqrt{2}$ +3 $\sqrt{3}$ =5 $\sqrt{5}$ D、 $\sqrt{6}$ ÷ $\sqrt{3}$ = $\sqrt{2}$

查看试题解析
5. 在今年“全国助残日”捐款活动中，某班级第一小组7名同学积极捐出自己的零花钱，奉献自己的爱心，他们捐款的数额分别是（单位：元）50、20、50、30、25、50、55，这组数据的众数和中位数分别是（）

A、50元，30元 B、50元，40元 C、50元，50元 D、55元，50元

查看试题解析
6. 为了开展阳光体育活动，某班计划购买毽子和跳绳两种体育用品，共花费35元，毽子单价3元，跳绳单价5元，购买方案有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
7. 若|3﹣a|+ $\sqrt{2 + b}$ =0，则a+b的值是（）

A、2 B、1 C、0 D、﹣1

查看试题解析
8. 同一直角坐标系中，一次函数y₁=k₁x+b与正比例函数y₂=k₂x的图象如图所示，则满足y₁≥y₂的x取值范围是（）

A、x≤﹣2 B、x≥﹣2 C、x＜﹣2 D、x＞﹣2

查看试题解析
9. 如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（）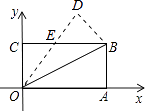

A、（4，8） B、（5，8） C、（ $\frac{24}{5}$ ， $\frac{32}{5}$ ） D、（ $\frac{22}{5}$ ， $\frac{36}{5}$ ）

查看试题解析
10. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距300千米；
②乙车比甲车晚出发1小时，却早到1小时；
③乙车出发后2.5小时追上甲车；
④当甲、乙两车相距50千米时，t= $\frac{5}{4}$ 或 $\frac{15}{4}$ ．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

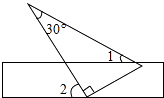
11. 25的算术平方根是．

查看试题解析
12. 如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为．

查看试题解析
13. 在平面直角坐标系中，将直线l₁：y=﹣2x﹣2向右平移单位后，得到直线l₂：y=﹣2x+4．

查看试题解析
14. 如图是“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=10，EF=2，那么AH等于

查看试题解析

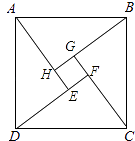
三、解答题

15. 计算与解方程组

(1)、计算： $\frac{\sqrt{27} + \sqrt{48}}{\sqrt{3}}$ ；

(2)、计算： $(\sqrt{2} + \sqrt{3}) (\sqrt{2} - \sqrt{3})$

(3)、计算： $\sqrt{2} - 3 \times \sqrt{\frac{1}{3}} + \sqrt[3]{- 8} - {(π + 1)}^{0} \times {(\frac{1}{\sqrt{3}})}^{- 1}$ ；

(4)、解方程组 ${\begin{matrix} 2 x - y = 5 \\ 3 x - 2 y = 8 \end{matrix}$ ．

查看试题解析
16. 如图，有两条公路OM、ON相交成30°角，沿公路OM方向离O点80米处有一所学校A．当重型运输卡车P沿道路ON方向行驶时，在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大．若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时．

(1)、求对学校A的噪声影响最大时卡车P与学校A的距离；

(2)、求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间．

查看试题解析
17. 小华从家里到学校的路是一段平路和一段下坡路，假设他始终保持平路每分钟走60m，下坡路每分钟走80m，上坡路每分钟走40m，则他从家里到学校需10min，从学校到家里需15min．问：从小华家到学校的平路和下坡路各有多远？

查看试题解析
18. 某商场统计了今年1～5月A，B两种品牌冰箱的销售情况，并将获得的数据绘制成折线统计图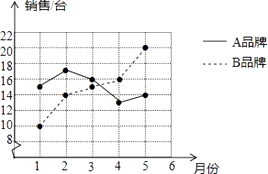

(1)、分别求该商场这段时间内A，B两种品牌冰箱月销售量的中位数和方差；

(2)、根据计算结果，比较该商场1～5月这两种品牌冰箱月销售量的稳定性．

查看试题解析
19. 兰新铁路的通车，圆了全国人民的一个梦，坐上火车去观赏青海门源百里油菜花海，感受大美青海独特的高原风光，暑假某校准备组织学生、老师到门源进行社会实践，为了便于管理，师生必须乘坐在同一列高铁上，根据报名人数，若都买一等座单程火车票需2340元，若都买二等座单程火车票花钱最少，则需1650元：
西宁到门源的火车票价格如下表
运行区间
票价
上车站
下车站
一等座
二等座
西宁
门源
36元
30元

(1)、参加社会实践的学生、老师各有多少人？

(2)、由于各种原因，二等座火车票单程只能买x张（参加社会实践的学生人数＜x＜参加社会实践的总人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐并且总费用最低的前提下，请你写出购买火车票的总费用（单程）y与x之间的函数关系式．

查看试题解析
20. 阅读材料：善于思考的小军在解方程组 ${\begin{matrix} 2 x + 5 y = 3 ① \\ 4 x + 11 y = 5 ② \end{matrix}$ 时，采用了一种“整体代换”的解法：
解：将方程②变形：4x+10y+y=5 即2（2x+5y）+y=5③
把方程①代入③得：2×3+y=5，∴y=﹣1
把y=﹣1代入①得x=4，∴方程组的解为 ${\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$ ．
请你解决以下问题：

(1)、模仿小军的“整体代换”法解方程组 ${\begin{matrix} 3 x - 2 y = 5 ① \\ 9 x - 4 y = 19 ② \end{matrix}$

(2)、已知x，y满足方程组 ${\begin{matrix} 3 x^{2} - 2 x y + 12 y^{2} = 5 ① \\ 2 x^{2} + x y + 8 y^{2} = 36 ② \end{matrix}$ ．
（i）求x²+4y²的值；
（ii）求 $\frac{1}{x}$ + $\frac{1}{2 y}$ 的值．

查看试题解析
21. 如图，在平面直角坐标系xOy中，已知正比例函数y= $\frac{3}{4}$ x与一次函数y=﹣x+7的图象交于点A．

(1)、求点A的坐标；

(2)、设x轴上有一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交y= $\frac{3}{4}$ x和y=﹣x+7的图象于点B，C，连接OC．若BC= $\frac{7}{5}$ OA，求△OBC的面积．

查看试题解析

运行区间		票价
上车站	下车站	一等座	二等座
西宁	门源	36元	30元