2015-2016学年广东省深圳市龙岗区八年级上学期期末数学试卷

试卷更新日期：2016-12-30 类型：期末考试

进入出卷网下载

一、选择题

1. 数学 $\sqrt{2}$ ， $\frac{1}{3}$ ，π， $\sqrt[3]{8}$ ，0. $\dot{3}$ 中无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下列长度的线段不能构成直角三角形的是（）

A、8，15，17 B、1.5，2，3 C、6，8，10 D、5，12，13

查看试题解析
3. 如图，笑脸盖住的点的坐标可能为（）

A、（5，2） B、（3，﹣4） C、（﹣4，﹣6） D、（﹣1，3）

查看试题解析
4. 点M（2，1）关于x轴对称的点的坐标是（）

A、（1，﹣2） B、（﹣2，1） C、（2，﹣1） D、（﹣1，2）

查看试题解析
5. 下列各式中，正确的是（）

A、 $\sqrt{16}$ =±4 B、± $\sqrt{16}$ =4 C、 $\sqrt[3]{- 27}$ =﹣3 D、 $\sqrt{{(- 4)}^{2}}$ =﹣4

查看试题解析
6. 若函数y=（k﹣1）x^|k|+b+1是正比例函数，则k和b的值为（　　）

A、k=±1，b=﹣1 B、k=±1，b=0 C、k=1，b=﹣1 D、k=﹣1，b=﹣1

查看试题解析
7. 在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（）

A、 $\frac{36}{5}$ B、 $\frac{12}{25}$ C、 $\frac{9}{4}$ D、 $\frac{3 \sqrt{3}}{4}$

查看试题解析
8. 下列命题中，不成立的是（）

A、两直线平行，同旁内角互补 B、同位角相等，两直线平行 C、一个三角形中至少有一个角不大于60度 D、三角形的一个外角大于任何一个内角

查看试题解析
9. 为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查．那么最终买什么水果，下面的调查数据中最值得关注的是（　　）

A、中位数 B、平均数 C、众数 D、加权平均数

查看试题解析
10. 2016年“龙岗年货博览会”在大运中心体育馆展销，小丽从家出发前去购物，途中发现忘了带钱，于是打电话让妈妈马上从家里送来，同时小丽也往回走，遇到妈妈后聊了一会儿，接着继续前往大运中心体育馆．设小丽从家出发后所用时间为t，小丽与体育馆的距离为S，下面能反映S与t的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
11. 如图，∠x的两条边被一直线所截，用含α和β的式子表示∠x为（）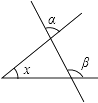

A、α﹣β B、β﹣α C、180°﹣α+β D、180°﹣α﹣β

查看试题解析
12. 如图，把一个等腰直角三角形放在间距是1的横格纸上，三个顶点都在横格上，则此三角形的斜边长是（）

A、3 B、 $\sqrt{10}$ C、2 $\sqrt{2}$ D、2 $\sqrt{3}$

查看试题解析

二、填空题

13. 16的平方根是．

查看试题解析
14. 数据3，4，6，8，x，7的众数是7，则数据4，3，6，8，2，x的中位数是．

查看试题解析
15. 观察下列各式： $\frac{1}{\sqrt{2} + 1}$ = $\sqrt{2}$ ﹣1， $\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\sqrt{3} - \sqrt{2}$ ， $\frac{1}{2 + \sqrt{3}}$ =2﹣ $\sqrt{3}$ …请利用你发现的规律计算：
（ $\frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{2 + \sqrt{3}}$ + $\frac{1}{\sqrt{5} + 2}$ +…+ $\frac{1}{\sqrt{2016} + \sqrt{2015}}$ ）×（ $\sqrt{2016}$ + $\sqrt{2}$ ）=

查看试题解析
16. 如图，在矩形ABCD中，AB=3，BC=4，现将点A，C重合，使纸片折叠压平，折痕为EF，那么重叠部分△AEF的面积= ．

查看试题解析

三、解答题

17. 计算： $\sqrt{8}$ ﹣| $\sqrt[3]{- 64}$ |﹣4 $\sqrt{\frac{1}{2}}$ + $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}}$ ．

查看试题解析
18. 解方程组： ${\begin{matrix} 0.5 x + 0.7 y = 35 \\ x + 0.4 y = 40 \end{matrix}$ ．

查看试题解析
19. 每年9月举行“全国中学生数学联赛”，成绩优异的选手可参加“全国中学生数学冬令营”，冬令营再选拔出50名优秀选手进入“国家集训队”．第31界冬令营已于2015年12月在江西省鹰谭一中成功举行．现将脱颖而出的50名选手分成两组进行竞赛，每组25人，成绩整理并绘制成如下的统计图：
请你根据以上提供的信息解答下列问题：

(1)、请你将表格补充完整：
平均数
中位数
众数
方差
一组
74
104
二组
72

(2)、从本次统计数据来看，组比较稳定．

查看试题解析
20. 已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．求证：AB∥CD．

查看试题解析
21. “双十一”当天，某淘宝网店做出优惠活动，按原价应付额不超过200元的一律9折优惠，超过200元的，其中200元按9折算，超过200元的部分按8折算．设某买家在该店购物按原价应付x元，优惠后实付y元．

(1)、当x＞200时，试写出y与x之间的函数关系式（如果是一次函数，请写成y=kx+b的形式）；

(2)、该买家挑选的商品按原价应付300元，求优惠后实付多少元？

查看试题解析
22. 如图，l₁反映了甲离开A地的时间与离A地的距离的关系l₂反映了乙离开A地的时间与离开A地距离之间的关系，根据图象填空：

(1)、当时间为0时，甲离A地千米；

(2)、当时间为时，甲、乙两人离A地距离相等；

(3)、图中P点的坐标是；

(4)、l₁对应的函数表达式是：S₁=；

(5)、当t=2时，甲离A地的距离是千米；

(6)、当S=28时，乙离开A地的时间是时．

查看试题解析
23.
如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（6，4），E为AB的中点，过点D（8，0）和点E的直线分别与BC、y轴交于点F，G．

(1)、求直线DE的函数关系式；

(2)、函数y=mx﹣2的图象经过点F且与x轴交于点H，求出点F的坐标和m值；

(3)、在（2）的条件下，求出四边形OHFG的面积．

查看试题解析

	平均数	中位数	众数	方差
一组	74			104
二组				72