2015-2016学年广东省深圳市福田区八年级上学期期末数学试卷

试卷更新日期：2016-12-30 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数是无理数的是（）

A、 $\sqrt{1}$ B、 $\frac{1}{3}$ C、3.14159 D、 $\sqrt{2}$

查看试题解析
2. 在平面直角坐标系中，点P（﹣3，4）关于x轴的对称点的坐标是（）

A、（﹣4，﹣3） B、（﹣3，﹣4） C、（3，4） D、（3，﹣4）

查看试题解析
3. 点A（1，y₁）、B（2，y₂）在直线y=2x+2上，y₁与y₂的大小关系是（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁=y₂ D、不能确定

查看试题解析
4. 若直角三角形的三边长分别为6、10、m，则m²的值为（）

A、8 B、64 C、136 D、136或64

查看试题解析
5. 方程组 ${\begin{matrix} x - y = 2 \\ 2 x + y = 1 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ B、 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$ C、 ${\begin{matrix} x = 0 \\ y = 1 \end{matrix}$ D、 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$

查看试题解析
6. 一组数据1，1，2，3，4，4，5，6的众数是（）

A、1 B、4 C、1和4 D、3.5

查看试题解析
7. 如图，对于图中标记的各角，下列条件能够推理得到a∥b的是（）

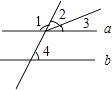A、∠1=∠4 B、∠2=∠4 C、∠3+∠2=∠4 D、∠2+∠3+∠4=180°

查看试题解析
8.
如图，动点P从（1，2）出发，沿图中箭头所示方向运动，每当碰到长方形的边时反弹（反弹时反射角等于入射角），假设反弹可以无限进行下去，则在点P运动路径上的点是（　　）

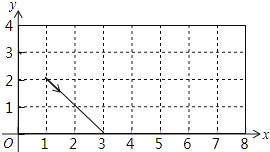A、（0，5） B、（5，0） C、（3，3） D、（7，3）

查看试题解析
9. 在坐标平面内有下列三条直线：
①经过点（0，2）且平行于x轴的直线；
②直线y=2x﹣8；
③经过点（0，12）且平行于直线y=﹣2x的直线，
其中经过点（5，2）但不经过第三象限的直线共有（）

A、0条 B、1条 C、2条 D、3条

查看试题解析
10. 若 $\sqrt{12}$ + $\sqrt{m}$ =n $\sqrt{3}$ （n为整数），则m的值可以是（）

A、 $\frac{1}{3}$ B、18 C、24 D、75

查看试题解析
11. 甘老师将一摞笔记本分给若干同学，每个同学5本，则剩下8本；每个同学8本，又差了7本，若设有x个同学，y本笔记本，则可得方程组（）

A、 ${\begin{matrix} y = 5 x + 8 \\ y + 7 = 8 x \end{matrix}$ B、 ${\begin{matrix} y = 5 x - 8 \\ y - 7 = 8 x \end{matrix}$ C、 ${\begin{matrix} x = 5 x + 8 \\ x + 7 = 8 y \end{matrix}$ D、 ${\begin{matrix} x = 5 x - 8 \\ x - 7 = 8 y \end{matrix}$

查看试题解析
12. 如图，平行于x轴的直线l与y轴、直线y=3x、直线y=x分别交于点A，B，C．则下列结论正确的个数有（）
①∠AOB+∠BOC=45°；②BC=2AB；③OB²=10AB²；④OC²= $\frac{8}{5}$ OB² ．

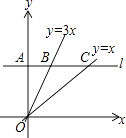A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. $\sqrt{4}$ 的算术平方根为．

查看试题解析
14. 对顶角相等的逆命题是命题（填写“真”或“假”）．

查看试题解析
15. 一副三角板如图所示叠放在一起，则图中∠ABC=

查看试题解析
16. 如图，直线l₁的表达式为y=﹣3x+3，且直线l₁与x轴交与点D，直线l₂经过点A，B，且与直线l₁交于点C，则△BDC的面积为．

查看试题解析

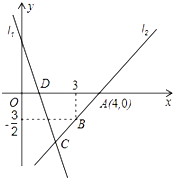
三、解答题

17. 计算：

(1)、 $\frac{\sqrt{20} - \sqrt{5}}{\sqrt{5}}$

(2)、（ $\sqrt{6}$ ﹣ $\sqrt{\frac{1}{6}}$ ）× $\sqrt{3}$ ﹣ $\frac{3}{2}$ $\sqrt{2}$ ．

查看试题解析
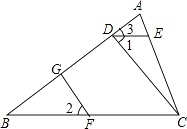
18. 解方程组： ${\begin{matrix} y = x - 4 \\ 5 x + 2 y = 6 \end{matrix}$ ．

查看试题解析
19. 如图所示，现有下列4个亊项：（1）∠1=∠2，（2）∠3=∠B，（3）FG⊥AB于G，（4）CD⊥AB于D．
以上述4个事项中的（1）、（2）、（3）三个作为一个命题的已知条件，（4）作为该命题的结论，可以组成一个真命题．请你证明这个真命题．

查看试题解析
20. 我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀，这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表（不完整）如下所示：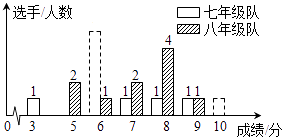
队别
平均分
中位数
方差
合格率
优秀率
七年级
m
3.41
90%
20%
八年级
7.1
n
80%
10%

(1)、观察条形统计图，可以发现：八年级成绩的标准差，七年级成绩的标准差（填“＞”、“＜”或“=”），表格中m= ， n=；

(2)、计算七年级的平均分；

(3)、有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．

查看试题解析
21. 某服装店用7000元购进A，B两种新式服装，按标价售出后获得毛利润4000元（毛利润=售价﹣进价），这两种服装的进价，标价如表所示：
类型
价格
A型
B型
进价（元/件）
60
100
标价（元/件）
100
150
求这两种服装各购进的件数？

查看试题解析
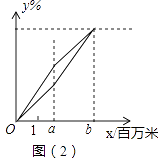
22. 如图，是一个圆柱形的饼干盒，在盒子外侧下底面的点A处有甲、乙两只蚂蚁，它们都想要吃到上底面外侧B′处的食物：甲蚂蚁沿A→A′→B′的折线爬行，乙蚂蚁沿圆柱的侧面爬行：若∠AOB=∠A′O′B′=90°（AA′、BB′都与圆柱的中轴线OO′平行），圆柱的底面半径是12cm，高为1cm，则：

(1)、A′B′=cm，甲蚂蚁要吃到食物需爬行的路程长l₁=cm；

(2)、乙蚂蚁要吃到食物需爬行的最短路程长l₂=cm（π取3）；

(3)、若两只蚂蚁同时出发，且爬行速度相同，在乙蚂蚁采取最佳策略的前提下，哪只蚂蚁先到达食物处？请你通过计算或合理的估算说明理由．（参考数据：π取3， $\sqrt{2}$ ≈1.4）

查看试题解析
23. 二轮自行车的后轮磨损比前轮要大，当轮胎的磨损度（%）达到100时，轮胎就报废了，当两个轮的中的一个报废后，自行车就不可以继续骑行了．过去的资料表明：把甲、乙两个同质、同型号的新轮胎分别安装在一个自行车的前、后轮上后，甲、乙轮胎的磨损度（%）y₁、y₂与自行车的骑行路程x （百万米）都成正比例关系，如图（1）所示：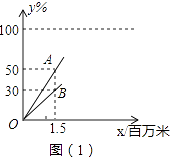

(1)、线段OB表示的是（填“甲”或“乙”），它的表达式是（不必写出自变量的取值范围）；

(2)、求直线OA的表达式，根据过去的资料，这辆自行车最多可骑行多少百万米？

(3)、爱动脑筋的小聪，想了一个增大自行车骑行路程的方案：如图（2），当自行车骑行a百万米后，我们可以交换自行车的前、后轮胎，使得甲、乙两个轮胎在b百万米处，同时报废，请你确定方案中a、b的值．

查看试题解析

队别	平均分	中位数	方差	合格率	优秀率
七年级		m	3.41	90%	20%
八年级	7.1	n		80%	10%