2015-2016学年广东省深圳市宝安区八年级上学期期末数学试卷

试卷更新日期：2016-12-30 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数中，无理数的是（）

A、 $\sqrt{6}$ B、 $\sqrt{25}$ C、 $\frac{7}{13}$ D、3.1415

查看试题解析
2. 在军事演习中，利用雷达跟踪某一“敌方”目标，需要确定该目标的（　　）

A、方向 B、距离 C、大小 D、方向与距离

查看试题解析
3. 一次函数 $y = \frac{1}{2} x - 1$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 在直角坐标系中，点A（a，3）与点B（﹣4，b）关于y轴对称，则a+b的值是（）

A、﹣7 B、﹣1 C、1 D、7

查看试题解析
5. 已知x=1，y=2是方程ax+y=5的一组解，则a的值是（）

A、﹣3 B、﹣2 C、3 D、7

查看试题解析
6.
如图所示：某商场有一段楼梯，高BC=6m，斜边AC是10米，如果在楼梯上铺上地毯，那么需要地毯的长度是（　　）

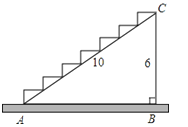A、8m B、10m C、14m D、24m

查看试题解析
7. 某特警队为了选拔“神枪手”，甲、乙、丙、丁四人进入射击比赛，每人10次射击成绩的平均数都是9.8环，方差分别为S_甲²=0.63，S_乙²=0.51，S_丙²=0.42，S_丁²=0.45，则四人中成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图，AB∥CD，EF与AB，CD分别相交于点E，F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP=40°，则∠EPF的度数是（）

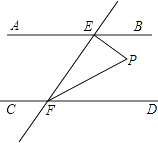A、25° B、65° C、75° D、85°

查看试题解析
9. 下列命题中，假命题的是（）

A、同旁内角相等，两直线平行 B、等腰三角形的两个底角相等 C、同角（等角）的补角相等 D、三角形的一个外角大于任何一个与它不相邻的内角

查看试题解析
10. 2015年亚洲杯足球冠军联赛恒大队广州主场，小李在网上预订了小组赛和淘汰赛两个阶段的球票共10张，总价为5600元．其中小组赛球票每张500元，淘汰赛每张800元，问小李预定了小组赛和淘汰赛的球票各多少张？设小李预定了小组赛球票x张，淘汰赛球票y张，可列方程组（）

A、 ${\begin{matrix} x + y = 5600 \\ 500 x + 800 y = 10 \end{matrix}$ B、 ${\begin{matrix} x + y = 10 \\ 800 x + 500 y = 5600 \end{matrix}$ C、 ${\begin{matrix} x + y = 10 \\ 500 x + 800 y = 5600 \end{matrix}$ D、 ${\begin{matrix} x + y = 10 \\ 500 x - 800 y = 5600 \end{matrix}$

查看试题解析
11. 如图，长方形ABCD的边AB=1，BC=2，AP=AC，则点P所表示的数是（）

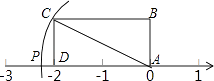A、5 B、﹣2.5 C、 $\sqrt{5}$ D、- $\sqrt{5}$

查看试题解析
12. 一辆汽车在行驶过程中，路程y（千米）与时间x（小时）之间的函数关系如图4所示，已知开始1小时的行驶速度是60千米/时，那么1小时以后的速度是（）

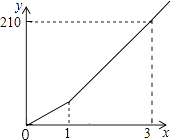A、70千米/时 B、75千米/时 C、105千米/时 D、210千米/时

查看试题解析

二、填空题

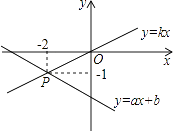
13. 9的算术平方根是．

查看试题解析
14. 如图，已知函数y=ax+b和y=kx的图象交于点P，根据图象可得，二元一次方程组 ${\begin{matrix} y = a x + b \\ y = k x \end{matrix}$ 的根是

查看试题解析
15. 去年“双11”购物节的快递量暴增，某快递公司要在街道旁设立一个派送还点，向A，B两居民区投送快递，派送点应该设在什么地方，才能使它到A，B的距离之和最短？快递员根据实际情况，以街道为x轴，建立了如图所示的平面直角坐标系，测得坐标A（﹣2，2）、B（6，4），则派送点的坐标是

查看试题解析
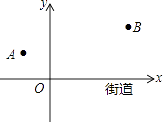16. 如图，△ABC中，AB=6，BC=8，AC=10，把△ABC沿AP折叠，使边AB与AC重合，点B落在AC边上的B′处，则折痕AP的长等于．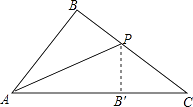

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{2} (\sqrt{5} + \sqrt{2}) + {(- π)}^{0}$

(2)、 $\sqrt{27} - 6 \sqrt{\frac{1}{3}} + \sqrt[3]{- 8}$ ．

查看试题解析
18. 解方程组

(1)、 ${\begin{matrix} y = 2 x - 3 \\ x + 2 y = 14 \end{matrix}$

(2)、 ${\begin{matrix} 3 x - y = - 5 \\ 2 x + 3 y = 4 \end{matrix}$ ．

查看试题解析
19. 迎接学校“元旦”文艺汇演，八年级某班的全体同学捐款购买了表演道具，经过充分的排练准备，最终获得了一等奖．班长对全体同学的捐款情况绘制成下表：
捐款金额
5元
10元
15元
20元
捐款人数
10人
15人
5人
由于填表时不小心把墨水滴在了统计表上，致使表中数据不完整，但知道捐款金额为10元的人数为全班人数的30%，结合上表回答下列问题：

(1)、该班共有名同学；

(2)、该班同学捐款金额的众数是元，中位数是元．

(3)、如果把该班同学的捐款情况绘制成扇形统计图，则捐款金额为20元的人数所对的扇形圆心角为度．

查看试题解析
20. 如图，四边形ABCD中，点F是BC中点，连接AF并延长，交于DC的延长线于点E，且∠1=∠2．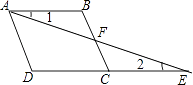

(1)、求证：△ABF≌△ECF；

(2)、若AD∥BC，∠B=125°，求∠D的度数．

查看试题解析
21. 列方程解应用题：
小张第一次在商场购买A，B两种商品各一件，花费60元；第二次购买时，发现两种商品的价格有了调整：A商品涨价20%，B商品降价10%，购买A，B两种商品各一件，同样花费60元．求A，B两种商品原来的价格．

查看试题解析
22. 某专营商场销售一种品牌电脑，每台电脑的进货价是0.4万元．图中的直线l₁表示该品牌电脑一天的销售收入y₁（万元）与销售量x（台）的关系，已知商场每天的房租、水电、工资等固定支出为3万元．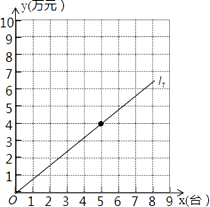

(1)、直线l₁对应的函数表达式是，每台电脑的销售价是万元；

(2)、写出商场一天的总成本y₂（万元）与销售量x（台）之间的函数表达式：；

(3)、在图的直角坐标系中画出第（2）小题的图象（标上l₂）；

(4)、通过计算说明：每天销售量达到多少台时，商场可以盈利．

查看试题解析
23.
如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．

(1)、求对角线AB所在直线的函数关系式；

(2)、对角线AB的垂直平分线MN交x轴于点M，连接AM，求线段AM的长；

(3)、若点P是直线AB上的一个动点，当△PAM的面积与长方形OABC的面积相等时，求点P的坐标．

查看试题解析

捐款金额	5元	10元	15元	20元
捐款人数	10人	15人		5人