河南省平顶山市2018届九年级数学中招调研试卷（一）

试卷更新日期：2018-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，绝对值最小的数是（）

A、π B、 $\frac{1}{2}$ C、-2 D、- $\frac{1}{3}$

查看试题解析
2. 下列运算正确的是（）

A、 $2 a^{3} + 3 a^{2} = 5 a^{5}$ B、 $3 a^{3} b^{2} \div a^{2} b = 3 a b$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(- a)}^{3} + a^{3} = 2 a^{3}$

查看试题解析
3. 已知关于x的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有实数根，若k为非负整数，则k等于（）

A、0 B、1 C、0，1 D、2

查看试题解析
4. 不等式组 ${\begin{matrix} 3 x - 1 > 2 \\ 2 - x \geq 0 \end{matrix}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
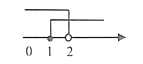
5. 一个不透明的袋子里装有质地、大小都相同的3个红球和1个绿球；随机从中摸出一球，不再放回，充分搅均后再随机摸出一球。则两次都摸到红球的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
6. 如图，BE∥AF，点D是AB上一点，且DC⊥BE于点C，若∠A=35°，则∠ADC的度数（）

A、105° B、115° C、125° D、135°

查看试题解析
7. 如图，在平行四边形ABCD中，点E是边AD上一点，且AE=2ED，EC交对角线BD于点F，则 $\frac{E F}{F C}$ 等于（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
8. 如图，已知AB是⊙O直径，BC是弦，∠ABC=40°，过圆心O作OD⊥BC交弧BC于点D，连接DC，则∠DCB为（）

A、20° B、25° C、30° D、35°

查看试题解析
9. 已知一次函数y=(k+1)x+b的图象与x轴负半轴相交，且函数值y随自变量x的增大而增大，则k，b的取值情况为（）

A、k>−1，b>0 B、k>−1，b<0 C、k<−1，b>0 D、k<−1，b<0

查看试题解析
10. 如图，已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象与x轴交于A，B两点，对称轴为直线x=2，下列结论：①abc>0； ②4a+b=0；③若点A坐标为(−1，0)，则线段AB=5； ④若点M(x₁ ， y₁)、N(x₂ ， y₂)在该函数图象上，且满足0<x₁<1，2<x₂<3，则y₁<y₂其中正确结论的序号为（）

A、①，② B、②，③ C、③，④ D、②，④

查看试题解析

二、填空题

11. 计算： $2^{- 2} + {(\sqrt{4} - 1)}^{0}$ ＝

查看试题解析
12. 方程 $\frac{x}{x - 1} - \frac{2}{x} = 1$ 的解为

查看试题解析
13. 如图，在平面直角坐标系中，函数y=kx+b(k≠0)与 $y = \frac{m}{x}$ (m≠0)的图象相交于点A(2，3)，B(−6，−1)。则关于x的不等式kx+b> $\frac{m}{x}$ 的解集是

查看试题解析
14. 如图，在矩形ABCD中，AB=6，E，H分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BH上的F处，则AD＝

查看试题解析
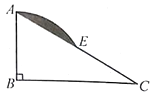
15. 如图，在Rt△ABC中，∠B=90°，∠C=30°，BC= $\sqrt{3}$ ，以点B为圆心，AB为半径作弧交AC于点E，则图中阴影部分面积是

查看试题解析

三、解答题

16. 化简 $\frac{x - 3}{x^{2} - 4} \div (\frac{x^{2} - 2 x}{x^{2} - 4 x + 4} - \frac{3}{x - 2})$ ，并从1，2，3，−2四个数中，取一个合适的数作为x的值代入求值。

查看试题解析
17. 为了解家长对“学生在校带手机”现象的看法，某校“九年级兴趣小组”随机调查了该校学生家长若干名，并对调查结果进行整理，绘制如下不完整的统计图：

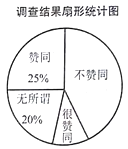
请根据以上信息，解答下列问题

(1)、这次接受调查的家长总人数为人；

(2)、在扇形统计图中，求“很赞同”所对应的扇形圆心角的度数；

(3)、若在这次接受调查的家长中，随机抽出一名家长，恰好抽到“无所谓”的家长概率是多少?

查看试题解析
18. 如图，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于点B，且四边形BCOE是平行四边形。

(1)、BC是⊙O的切线吗?若是，给出证明：若不是，请说明理由；

(2)、若⊙O半径为1，求AD的长。

查看试题解析
19. 如图，湛河两岸AB与EF平行，小亮同学假期在湛河边A点处，测得对岸河边C处视线与湛河岸的夹角∠CAB=37°，沿河岸前行140米到点B处，测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据：sin37°≈0.60，cos37°=0.80，tan37°=0.75)

查看试题解析
20. 平高集团有限公司准备生产甲、乙两种开关，共8万件，销往东南亚国家和地区。已知2件甲种开关与3件乙种开关销售额相同；3件甲种开关比2件乙种开关的销售额多1500元。

(1)、甲种开关与乙种开关的销售单价各为多少元?

(2)、若甲、乙两种开关的销售总收入不低于5400万元，则至少销售甲种开关多少万件？

查看试题解析
21. 如图，直线y=2x与反比例函数 $y = \frac{k}{x}$ (k≠0，x>0)的图象交于点A(1，m)，点B(n，t)是反比例函数图象上一点，且n=2t。

(1)、求k的值和点B坐标；

(2)、若点P在x轴上，使得△PAB的面积为2，直接写出点P坐标。

查看试题解析
22. 如图1，正方形ABCD和正方形AEFG，连接DG，BE。

(1)、发现
当正方形AEFG绕点A旋转，如图2，①线段DG与BE之间的数量关系是②直线DG与直线BE之间的位置关系是

(2)、探究
如图3，若四边形ABCD与四边形AEFG都为矩形，且AD=2AB，AG=2AE，证明：直线DG⊥BE

(3)、应用
在(2)情况下，连结GE(点E在AB上方)，若GE∥AB，且AB= $\sqrt{5}$ ，AE=1，则线段DG是多少?(直接写出结论)

查看试题解析
23. 如图，抛物线y=ax²+bx(a≠0)的图象过原点O和点A(1， $\sqrt{3}$ )，且与x轴交于点B，△AOB的面积为 $\sqrt{3}$ 。

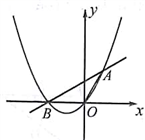
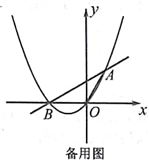(1)、求抛物线的解析式；

(2)、若抛物线的对称轴上存在一点M，使△AOM的周长最小，求M点的坐标；

(3)、点F是x轴上一动点，过F作x轴的垂线，交直线AB于点E，交抛物线于点P，且PE= $\frac{2 \sqrt{3}}{3}$ ，直接写出点E的坐标(写出符合条件的两个点即可)。

查看试题解析