广东省深圳市南山区2018届九年级下学期数学中考二模试卷
试卷更新日期：2018-05-28 类型：中考模拟
一、选择题
-
1. -5的相反数是（ ）A、－5 B、5 C、- D、2. 下列图案中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 要使二次根式 有意义，则x的取值范围是（ ）A、x≠1 B、x＞1 C、x≥1 D、x≠－14. 下列计算正确的是（ ）A、(－x2)3 ＝x5 B、x8 ÷x4 ＝x2 C、x3 ＋3x3 ＝3x6 D、(－x2)3 ＝－x65. 下列说法正确的是（ ）A、要了解人们对“低碳生活”的了解程度，宜采用普查方式 B、一组数据5，5，6，7的众数和中位数都是5 C、必然事件发生的概率为100% D、若甲组数据的方差是3.4，乙组数据的方差是1.68，则甲组数据比乙组数据稳定6. 下列命题中，是假命题的是（ ）A、对顶角相等 B、同旁内角相等 C、两点确定一条直线 D、角平分线上的点到角两边的距离相等7. 如图，将线段AB绕点O顺时针旋转90°得到线段A'B'，那么A(－2，5)的对应点A′的坐标是（ ）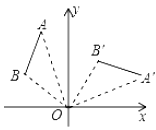
A、(2，5) B、(5， 2) C、(2，－5) D、(5，－2)8. 如图，用尺规作出了BF∥OA，作图痕迹中，弧MN是（ ）
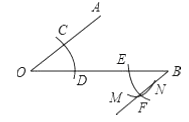A、以B为圆心，OD长为半径的弧 B、以C为圆心，CD长为半径的弧 C、以E为圆心，DC长为半径的弧 D、以E为圆心，OD长为半径的弧9. 如图，将平行四边形ABCD绕点A逆时针旋转40°，得到平行四边形AB′C′D′，若点B′恰好落在BC边上，则∠DC′B′的度数为（ ）
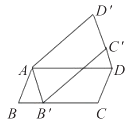A、60° B、65° C、70° D、75°10. 如图，小强从热气球上测量一栋高楼顶部B的仰角为30°，测量这栋高楼底部C的俯角为60°，热气球与高楼的水平距离为45米，则这栋高楼高为（ ）米
A、15 B、30 C、45 D、6011. 如图，已知矩形ABCD中，AB＝2，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点处，若四边形EFDC与矩形ABCD相似，则AD＝（ ）
A、 B、 ＋1 C、4 D、212. 如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，AB＝AE，AC＝AD．那么在下列四个结论中：(1)AC⊥BD；(2)BC＝DE；(3)∠DBC＝ ∠DAB；(4)△ABE是正三角形．其中一定正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 分解因式：ax2 －2a2 x＋a3 ＝ ．
14. 一个扇形的弧长是20π，面积是240π，则此扇形的圆心角为度．
15. 方程(m＋1)x2＋2x－1＝0有两个不相等的实数根，则m的范围为 ．
16. 如图，四边形ABCD为菱形，E为对角线BD延长线上一点，BD＝4，DE＝1，∠BAE＝45°，则AB长为 ．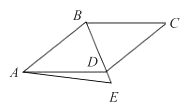
三、解答题
-
17. 计算： ＋|1－ |－（ ）-2-tan6018. 先化简，再求值(2－ )÷ ，其中x＝1＋ ．19. 中考即将来临，小王调查了初三年级部分同学在中考后将以何种方式对自己的老师表达感谢，他将调查结果分为如下四类：A类—当面表示感谢、B类—打电话表示感谢、C类—发短信表示感谢、D类—写书信表示感谢．他将调查结果绘制成了如图所示的扇形统计图和条形统计图．请你根据图中提供的信息完成
下列各题：
(1)、补全条形统计图；(2)、在A类的同学中，有4人来自同一班级，其中有2个女生．现准备从他们4人中随机抽出两位同学主持感谢恩师主题班会课，请用树状图或列表法求抽出1男1女的概率．20. 如图，已知一次函数y＝kx＋b(k≠0)的图象与反比例函数y= 的图象交于A、B两点，分别与x轴、y轴交于点C、D，点B的横坐标为1，OC＝OD，点P在反比例函数图象上且到x轴、y轴距离相等．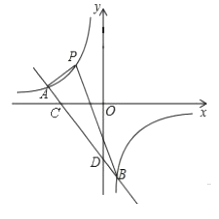
(1)、求一次函数的解析式；(2)、求△APB的面积．21. 某公司经市场调查发现，该公司生产的某商品在第x天的售价(1≤x≤100)为(x＋30)元/件，而该商品每天的销售量y(件)满足关系式：y＝220－2x，如果该商品第15天的售价按8折出售，仍然可以获得20%的利润．
(1)、求该公司生产每件商品的成本为多少元；(2)、问销售该商品第几天时，每天的利润最大？最大利润是多少？(3)、该公司每天需要控制人工、水电和房租支出共计a元，若考虑这一因素后公司对最大利润要控制在4000元至4500元之间(包含4000和4500)，且保证至少有90天的盈利，请直接写出a的取值范围．
22. 如图1，等腰△ABC中，AC＝BC，点O在AB边上，以O为圆心的圆与AC相切于点C，交AB边于点D，EF为⊙O的直径，EF⊥BC于点G．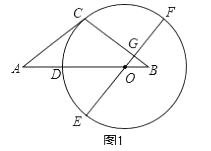
(1)、求证：D是弧EC的中点；(2)、如图2，延长CB交⊙O于点H，连接HD交OE于点K，连接CF，求证：CF＝OK＋DO；
(3)、如图3，在(2)的条件下，延长DB交⊙O于点Q，连接QH，若DO＝ ，KG＝2，求QH的长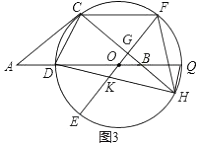
23. 已知，如图1，抛物线y＝ax2＋bx＋3与x轴交于点B、C，与y轴交于点A，且AO＝CO，BC＝4．
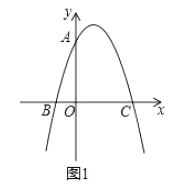(1)、求抛物线解析式；(2)、如图2，点P是抛物线第一象限上一点，连接PB交y轴于点Q，设点P的横坐标为t，线段OQ长为d，求d与t之间的函数关系式；
(3)、在(2)的条件下，过点Q作直线l⊥y轴，在l上取一点M(点M在第二象限)，连接AM，使AM＝PQ，连接CP并延长CP交y轴于点K，过点P作PN⊥l于点N，连接KN、CN、CM．若∠MCN＋∠NKQ＝45°时，求t值．