浙江省杭州市富阳区2018届九年级下学期数学中考一模试卷
试卷更新日期:2018-05-28 类型:中考模拟
一、仔细选一选
-
1. 计算 =( )A、 B、1 C、 D、2. 数据2, 5, 6, 0, 6, 1, 8的中位数是( )A、0 B、1 C、5 D、63. 下列计算正确的是( )A、 B、 C、 D、4. 如图,⊙ 是 的外接圆,则点 是 的( )
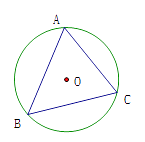 A、三条高线的交点 B、三条边的垂直平分线的交点 C、三条中线的交点 D、三角形三内角角平分线的交点5. 小马虎同学在解关于 的方程 时,误将 看成 ,得方程的解 ,则原方程正确的解为( )A、 B、2 C、 D、6. 如图,在 中,∠ABC=110°, ,则 =( )
A、三条高线的交点 B、三条边的垂直平分线的交点 C、三条中线的交点 D、三角形三内角角平分线的交点5. 小马虎同学在解关于 的方程 时,误将 看成 ,得方程的解 ,则原方程正确的解为( )A、 B、2 C、 D、6. 如图,在 中,∠ABC=110°, ,则 =( )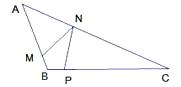 A、25° B、30° C、35° D、45°7. 如图是几何体的三视图及相关数据,则下列判断错误的是( )
A、25° B、30° C、35° D、45°7. 如图是几何体的三视图及相关数据,则下列判断错误的是( )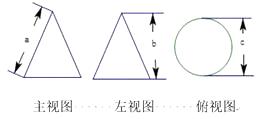 A、 B、 C、 D、8. 如图,线段 是⊙ 的直径,弦 ,垂足为 ,点 是 上任意一点, ,则 的值为( )
A、 B、 C、 D、8. 如图,线段 是⊙ 的直径,弦 ,垂足为 ,点 是 上任意一点, ,则 的值为( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,四边形 是菱形,∠B=60°,反比例函数 的图象经过点 ,若将菱形向下平移2个单位,点 恰好落在反比例函数的图象上,则反比例函数的表达式为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,四边形 是菱形,∠B=60°,反比例函数 的图象经过点 ,若将菱形向下平移2个单位,点 恰好落在反比例函数的图象上,则反比例函数的表达式为( )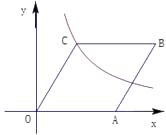 A、 B、 C、 D、10. 如图,在等边三角形 的内部,作 , 两两相交于 三点( 三点不重合).设 ,则下列关系正确的是( )
A、 B、 C、 D、10. 如图,在等边三角形 的内部,作 , 两两相交于 三点( 三点不重合).设 ,则下列关系正确的是( )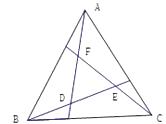 A、 B、 C、 D、
A、 B、 C、 D、二、认真填一填
-
11. 分解因式: = .12. 甲、乙、丙、丁参加体育训练,近期10次跳绳的平均成绩每分钟175个,其方差如下表所示:
选手
甲
乙
丙
丁
方差
0.023
0.017
0.021
0.019
则这10次跳绳中,这四个人中发挥最稳定的是 .
13. 估计 与 的大小关系是: (填“>”“=”或“<”)14. 如图,正六边形 的顶点 分别在正方形 的边 上.若 ,则 = .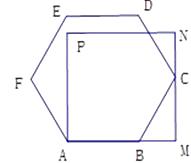 15. 已知二次函数 ,当 时,函数值 的最小值为 ,则 的值是 .
15. 已知二次函数 ,当 时,函数值 的最小值为 ,则 的值是 .
16. 如图,在矩形 中, 点 同时从点 出发,分别在 , 上运动,若点 的运动速度是每秒2个单位长度,且是点 运动速度的2倍,当其中一个点到达终点时,停止一切运动.以 为对称轴作 的对称图形 .点 恰好在 上的时间为秒.在整个运动过程中, 与矩形 重叠部分面积的最大值为 .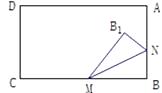
三、全面答一答
-
17. 解分式方程:18. 如图,已知
 (1)、只能用直尺和三角尺,过C点画CD∥AB,并保留作图痕迹.(2)、说明 的理由.19. 数学教师将班中留守学生的学习状况分成 四个等级,制成不完整的统计图:
(1)、只能用直尺和三角尺,过C点画CD∥AB,并保留作图痕迹.(2)、说明 的理由.19. 数学教师将班中留守学生的学习状况分成 四个等级,制成不完整的统计图: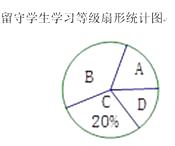
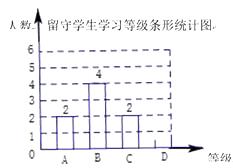 (1)、该班有多少名留守学生?并将该条形统计图补充完整.(2)、数学教师决定从 等级的留守学生中任选两名进行数学学习帮扶,使用列表或画树状图的方法,求出所选帮扶的两名留守学生来自同一等级的概率.20. 如图, 是⊙ 的直径, 是弦,连接 ,过点 的切线交 的延长线于点 ,
(1)、该班有多少名留守学生?并将该条形统计图补充完整.(2)、数学教师决定从 等级的留守学生中任选两名进行数学学习帮扶,使用列表或画树状图的方法,求出所选帮扶的两名留守学生来自同一等级的概率.20. 如图, 是⊙ 的直径, 是弦,连接 ,过点 的切线交 的延长线于点 ,且 .
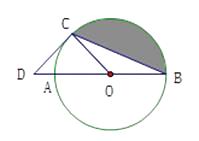 (1)、求劣弧 的长.(2)、求阴影部分弓形的面积.21. 直线 经过原点,若反比例函数 的图象与直线 相交于点 ,且点 的纵坐标是3.
(1)、求劣弧 的长.(2)、求阴影部分弓形的面积.21. 直线 经过原点,若反比例函数 的图象与直线 相交于点 ,且点 的纵坐标是3.
(1)、求 的值.(2)、结合图象求不等式 的解集.
22. 在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.(1)、求m的取值范围;(2)、若m取满足条件的最小的整数,①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n , 求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O . 设平移后的图象对应的函数表达式为y=a(x-h)2 +k , 当x<2时,y随x的增大而减小,求k的取值范围.
23. 如图,在 中, , 于点 ,点 在 上,且 ,连接 .
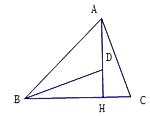 (1)、求证:(2)、如图,将 绕点 逆时针旋转 得到 (点 分别对应点 ), 设射线 与 相交于点 ,连接 ,试探究线段 与 之间满足的数量关系,并说明理由.
(1)、求证:(2)、如图,将 绕点 逆时针旋转 得到 (点 分别对应点 ), 设射线 与 相交于点 ,连接 ,试探究线段 与 之间满足的数量关系,并说明理由.