浙江省嘉兴市桐乡2018届初中毕业生学业考试适应性试卷(一)数学卷
试卷更新日期:2018-05-28 类型:中考模拟
一、选择题
-
1. -2的相反数是( )
A、 2 B、-2 C、 D、-2. 如图是一个水晶笔筒(在一个底面为正方形的长方体内部挖去一个圆柱),它的俯视图是( )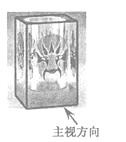 A、
A、 B、
B、 C、
C、 D、
D、 3. 若在实数范围内有意义,则n的取值范围是( )A、a>3 B、a<3 C、a≥3 D、a≤34. 下列计算正确的是( )A、x3+x3=x6 B、2x3-x3=x3 C、x2·x3=x6 D、(x2)3=x55. 两组数据:8,9,9,10和8.5,9,9,9.5,它们之间不相等的统计量是( )
3. 若在实数范围内有意义,则n的取值范围是( )A、a>3 B、a<3 C、a≥3 D、a≤34. 下列计算正确的是( )A、x3+x3=x6 B、2x3-x3=x3 C、x2·x3=x6 D、(x2)3=x55. 两组数据:8,9,9,10和8.5,9,9,9.5,它们之间不相等的统计量是( )
A、平均数 B、中位数 C、众数 D、方差6. 已知 ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A、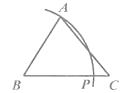 B、
B、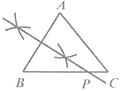 C、
C、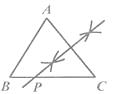 D、
D、 7. 如图,在Rt ABC中,∠ACB=900,BC=2.将 ABC绕顶点C逆时针旋转得到△ ,使点B’落在AC边上.设M是 的中点,连接BM,CM, BCM的面积为( )
7. 如图,在Rt ABC中,∠ACB=900,BC=2.将 ABC绕顶点C逆时针旋转得到△ ,使点B’落在AC边上.设M是 的中点,连接BM,CM, BCM的面积为( )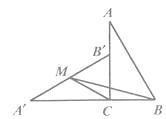 A、1 B、2 C、3 D、48. 关于x的方程(x-3)(x-5)=m(m>0)有两个实数根 , ( < ),则下列选项正确的是( )A、3< < <5 B、3< <5< C、 <2< <5 D、 <3且 >59. 如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子( )
A、1 B、2 C、3 D、48. 关于x的方程(x-3)(x-5)=m(m>0)有两个实数根 , ( < ),则下列选项正确的是( )A、3< < <5 B、3< <5< C、 <2< <5 D、 <3且 >59. 如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子( )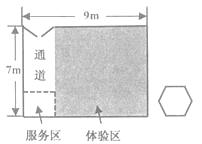 A、4张 B、5张 C、6张 D、7张10. 如图, ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A、4张 B、5张 C、6张 D、7张10. 如图, ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( ) A、 B、 C、2 D、2
A、 B、 C、2 D、2二、填空题
-
11. 已知 ,则 =
12. 计算:(x3+2x2)÷x2=
13. 清明节妈妈买了5只鲜肉粽、3只豆沙粽和2只蛋黄肉粽,粽子除了内部馅料不同外其它均相同.小王从中随机拿出1只,正好拿到鲜肉粽的概率是
14. 如图是一把折扇,其平面图是一个扇形,扇面ABDC的宽度AC是骨柄长OA的一半.已知OA=30 cm,∠AOB=120°,则扇面ABDC的周长为cm. 15. 如图,矩形ABCD中,E是AC的中点,点A、B在x轴上.若函数 的图像过D、E两点,则矩形ABCD的面积为 .
15. 如图,矩形ABCD中,E是AC的中点,点A、B在x轴上.若函数 的图像过D、E两点,则矩形ABCD的面积为 .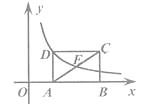 16. 如图, ABCD中,E是AD边上一点,AD=4 ,CD=3,ED= ,∠A=45 .点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将 CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为 .
16. 如图, ABCD中,E是AD边上一点,AD=4 ,CD=3,ED= ,∠A=45 .点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将 CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为 .
三、解答题
-
17. 解答题(1)、计算:( )2—2-1×(-6):(2)、解不等式:5x+2≤3(2+x),并把解在数轴上表示出来.
 18. 如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.
18. 如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.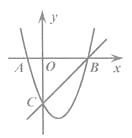 (1)、求直线BC的函数关系式;(2)、当y1>y2时,请直接写出x的取值范围.19. 对于实数m、n,我们定义一种运算“※”为:m※n=mn+m+n.
(1)、求直线BC的函数关系式;(2)、当y1>y2时,请直接写出x的取值范围.19. 对于实数m、n,我们定义一种运算“※”为:m※n=mn+m+n.
(1)、化简:(a+b)※(a一b);(2)、解关于x的方程:x※(1※x)=-1.20. 如图,已知AB是 的直径,C是 上一点,∠ACB的平分线交 于点D,
作PD∥AB,交CA的延长线于点P.连结AD,BD.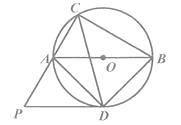
求证:
(1)、PD是 的切线;
(2)、21. 某市共有一中、二中、三中等3所高中,有一天所有高二学生参加了一次数学测试,阅卷后老师们对第10题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A(概念错误),B(计算错误),C(基本正确),D(完全正确).各校出现这四类情况的人数占本校高二学生数的百分比见下面的条形统计图: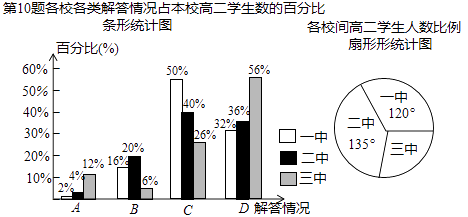
已知一中高二学生有400名,这三所学校之间高二学生人数的比例见扇形统计图.
(1)、求全市高二学生总数;(2)、求全市解答完全正确的高二学生数占高二学生总数的百分比;(3)、请你对三中高二数学老师提一个值得关注的教学建议,并说明理由.22. 有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮 。 与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.设AF∥MN.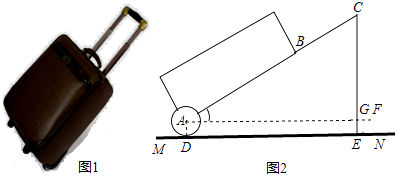
(1)、求(2)、当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,∠CAF=64° . 求此时拉杆BC的伸长距离.(精确到1cm,参考数据:sin64° 0.9,cos64°=0.39,tan64° 2.1)
23. 某公司对一款新高压锅进行测试,放入足量的水和设定某一模式后,在容积不变的情况下,根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小.压强在加热前是100kpa,达到最大值后高压锅停止加热。为方便分析,测试员记y=p-100,表示压强在测试过程中相对于100kpa的增加值.部分数据如下表:

温度f(℃)
0
10
20
30
40
50
60
压强增加值
Y(kpa)
0
9.5
18
25.5
32
37.5
42
(1)、根据表中的数据,在给出的坐标系中画出相应的点(坐标系已画在答卷上);(2)、y与t之间是否存在函数关系?若是,请求出函数关系式;否则请说明理由;(3)、①在该模式下,压强p的最大值是多少?②当t分别为,t1 , t2(t1<t2)时,对应y的值分别为y1 , y2 , 请比较 与 的大小,并解释比较结果的实际意义.
24. 小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF,把纸片展平;②沿折痕BG折叠纸片,使点C落在EF上的点P处,再折出PB、PC,最后用笔画出△PBC(图1). (1)、求证:图1中的 PBC是正三角形:(2)、如图2,小明在矩形纸片HIJK上又画了一个正三角形IMN,其中IJ=6cm,
(1)、求证:图1中的 PBC是正三角形:(2)、如图2,小明在矩形纸片HIJK上又画了一个正三角形IMN,其中IJ=6cm,且HM=JN.
①求证:IH=IJ
②请求出NJ的长;
(3)、小明发现:在矩形纸片中,若一边长为6cm,当另一边的长度a变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a的取值范围.