2016-2017学年山东省淄博市桓台二中高三上学期期中数学试卷

试卷更新日期：2016-12-28 类型：期中考试

进入出卷网下载

一、选择题

1. 集合M={x|lg（1﹣x）＜0}，集合N={x|﹣1≤x≤1}，则M∩N=（　　）

A、（0，1） B、[0，1） C、[﹣1，1] D、[﹣1，1）

查看试题解析
2. 函数f（x）= $\frac{\sqrt{2 - x}}{\lg x}$ 的定义域是（）

A、（0，2） B、（0，1）∪（1，2） C、（0，2] D、（0，1）∪（1，2]

查看试题解析
3. 下列命题中，真命题是（）

A、∀x∈R，2^x＞x² B、若a＞b，c＞d，则 a﹣c＞b﹣d C、∃x∈R，e^x＜0 D、ac²＜bc²是a＜b的充分不必要条件

查看试题解析
4. 已知平面向量 $\vec{a}$ =（﹣ $\sqrt{3}$ ，m）， $\vec{b}$ =（2，1）且 $\vec{a}$ ⊥ $\vec{b}$ ，则实数m的值为（）

A、 $- 2 \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $4 \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析
5. 若非零向量 $\vec{a}$ ， $\vec{b}$ 满足| $\vec{a}$ |= $\frac{2 \sqrt{2}}{3}$ | $\vec{b}$ |，且（ $\vec{a}$ ﹣ $\vec{b}$ ）⊥（3 $\vec{a}$ +2 $\vec{b}$ ），则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{2}$ C、 $\frac{3 π}{4}$ D、π

查看试题解析
6. 将函数y=sin（2x﹣ $\frac{π}{6}$ ）图象向左平移 $\frac{π}{4}$ 个单位，所得函数图象的一条对称轴的方程是（）

A、x= $\frac{π}{12}$ B、x= $\frac{π}{6}$ C、x= $\frac{π}{3}$ D、x=﹣ $\frac{π}{12}$

查看试题解析
7. 函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ $\frac{π}{2}$ ）的部分图象如图所示，则ω，φ的值分别为（）

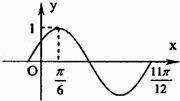A、2，0 B、2， $\frac{π}{4}$ C、2，﹣ $\frac{π}{3}$ D、2， $\frac{π}{6}$

查看试题解析
8. 设△ABC的内角A，B，C的对边分别为a，b，c．若a=2，c=2 $\sqrt{3}$ ，cosA= $\frac{\sqrt{3}}{2}$ ．且b＜c，则b=（）

A、3 B、2 $\sqrt{2}$ C、2 D、 $\sqrt{3}$

查看试题解析
9. 设函数f（x）=x³﹣12x+b，则下列结论正确的是（）

A、函数f（x）在（﹣∞，﹣1）上单调递增 B、函数f（x）在（﹣∞，﹣1）上单调递减 C、若b=﹣6，则函数f（x）的图象在点（﹣2，f（﹣2））处的切线方程为y=10 D、若b=0，则函数f（x）的图象与直线y=10只有一个公共点

查看试题解析
10. 设f（x）是定义在R上的偶函数，对任意的x∈R，都有f（x+4）=f（x），且当x∈[﹣2，0]时，f（x）=（ $\frac{1}{3}$ ）^x﹣6，若在区间（﹣2，6]内关于x的方程f（x）﹣log_a（x+2）=0（a＞1）恰有3个不同的实数根，求实数a的取值范围是（）

A、（1，2） B、（2，+∞） C、 $(1 ， \sqrt[3]{4})$ D、 $(\sqrt[3]{4} ， 2)$

查看试题解析

二、填空题

11. 2^﹣³ ， $3^{\frac{1}{2}}$ ，log₂5三个数中最大数的是．

查看试题解析
12. 已知奇函数f（x）满足对任意x∈R都有f（x+6）=f（x）成立，且f（1）=1，则f（2015）+f（2016）= ．

查看试题解析
13. 已知 $\vec{e}$ ₁ ， $\vec{e}$ ₂是平面单位向量，且 $\vec{e}$ ₁• $\vec{e}$ ₂= $\frac{1}{2}$ ，若平面向量 $\vec{b}$ 满足 $\vec{b}$ • $\vec{e}$ ₁= $\vec{b}$ • $\vec{e_{2}}$ =1，则| $\vec{b}$ |= ．

查看试题解析
14. 在三角形ABC中，acos（π﹣A）+bsin（ $\frac{π}{2}$ +B）=0，则三角形的形状为．

查看试题解析
15. 已知函数f（x）=2sin（x﹣ $\frac{π}{6}$ ）sin（x+ $\frac{π}{3}$ ），x∈R，则函数f（x）的最小正周期．

查看试题解析

三、解答题

16. 已知向量 $\vec{a}$ =（1，cos2x）， $\vec{b}$ =（sin2x，﹣ $\sqrt{3}$ ），函数f（x）=（1，cos2x）•（sin2x，﹣ $\sqrt{3}$ ）

(1)、若f（ $\frac{θ}{2}$ + $\frac{2 π}{3}$ ）= $\frac{6}{5}$ ，求cos2θ的值；

(2)、若x∈[0， $\frac{π}{2}$ ]，求函数f（x）的值域．

查看试题解析
17. 设f（x）是定义在（﹣∞，+∞）上的函数，对一切x∈R均有f（x）+f（x+3）=0，且当﹣1＜x≤1时，f（x）=2x﹣3．

(1)、求f（x）的周期；

(2)、求当2＜x≤4时，f（x）的解析式．

查看试题解析
18. 给出两个命题：
命题甲：关于x的不等式x²+（a﹣1）x+a²≤0的解集为∅；
命题乙：函数y=（2a²﹣a）^x为增函数．

(1)、甲、乙至少有一个是真命题；

(2)、甲、乙有且只有一个是真命题；
分别求出符合（1）（2）的实数a的取值范围．

查看试题解析
19. 已知向量 $\vec{a}$ =（1，2）， $\vec{b}$ =（﹣2，m）， $\vec{c}$ = $\vec{a}$ +（t²+1） $\vec{b}$ ， $\vec{c}$ =﹣k $\vec{a}$ + $\frac{1}{t}$ $\vec{b}$ ，m∈R，k、t为正实数．

(1)、若 $\vec{a}$ ∥ $\vec{b}$ ，求m的值；

(2)、若 $\vec{a}$ ⊥ $\vec{b}$ ，求m的值；

(3)、当m=1时，若 $\vec{x}$ ⊥ $\vec{y}$ ，求k的最小值．

查看试题解析
20. 在△ABC中，角A，B，C的对边分别是a、b、c，已知向量 $\vec{m}$ =（cosA，cosB）， $\vec{n}$ =（a，2c﹣b），且 $\vec{m}$ ∥ $\vec{n}$ ．

(1)、求角A的大小；

(2)、若a=4，求△ABC面积的最大值．

查看试题解析
21. 已知函数f（x）=1﹣ $\frac{a}{x}$ ﹣lnx（a∈R）．

(1)、当a=1时，求函数f（x）的图象在点（ $\frac{1}{2}$ ，f（ $\frac{1}{2}$ ））处的切线方程；

(2)、当a≥0时，记函数Γ（x）= $\frac{1}{2}$ ax²+（1﹣2a）x+ $\frac{a}{x}$ ﹣1+f（x），试求Γ（x）的单调递减区间；

(3)、设函数h（a）=3λa﹣2a²（其中λ为常数），若函数f（x）在区间（0，2）上不存在极值，求h（a）的最大值．

查看试题解析