2016-2017学年内蒙古包头市北重三中高二上学期期中数学试卷（理科）
试卷更新日期：2016-12-28 类型：期中考试
一、选择题：
-
1. 在空间直角坐标系中，点P（3，1，5）关于yOz平面对称的点的坐标为（ ）A、（﹣3，1，5） B、（﹣3，﹣1，5） C、（3，﹣1，﹣5） D、（﹣3，1，﹣5）2. 已知A（1，2）、B（﹣1，4）、C（5，2），则△ABC的边AB上的中线所在的直线方程为（ ）A、x+5y﹣15=0 B、x=3 C、x﹣y+1=0 D、y﹣3=03. 设圆的方程是x2+y2+2ax+2y+（a﹣1）2=0，0＜a＜1时原点与圆的位置关系是（ ）A、原点在圆上 B、原点在圆外 C、原点在圆内 D、不确定4. 直线 绕原点逆时针方向旋转30°后所得直线与圆（x﹣2）2+y2=3的位置关系是（ ）A、直线过圆心 B、直线与圆相交，但不过圆心 C、直线与圆相切 D、直线与圆无公共点5. 利用斜二测画法得到的：
①三角形的直观图是三角形；
②平行四边形的直观图是平行四边形；
③正方形的直观图是正方形；
④菱形的直观图是菱形．
以上结论，正确的是（ ）
A、①② B、① C、③④ D、①②③④6. 设空间四条直线a，b，c，d，满足a⊥b，b⊥c，c⊥d，d⊥a，下列命题中真命题是（ ）A、a⊥c B、b⊥d C、b∥d或a∥c D、b∥d且a∥c7. 已知直线l，m和平面α，则下列命题正确的是（ ）A、若l∥m，m⊂α，则l∥α B、若l∥α，m⊂α，则l∥m C、若l⊥m，l⊥α，则m⊥α D、若l⊥α，m⊂α，则l⊥m8. 正方体ABCD﹣A1B1C1D1中，M、N分别是CD、CC1的中点，则直线A1M与DN所成角的大小是（ ）A、 B、 C、 D、9. 如图，四棱锥S﹣ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（ ）
A、AC⊥SB B、AB∥平面SCD C、SA与平面SBD所成的角等于SC与平面SBD所成的角 D、AB与SC所成的角等于DC与SA所成的角10. 平面α过正方体ABCD﹣A1B1C1D1的顶点A，α∥平面CB1D1 ， α∩平面ABCD=m，α∩平面ABA1B1=n，则m、n所成角的正弦值为（ ）A、 B、 C、 D、11. 在棱长为a的正方体ABCD﹣A1B1C1D1中，P、Q是对角线A1C上两点，且 ，则三棱锥P﹣BDQ的体积为（ ）A、 B、 C、 D、无法确定12. 如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球半径为（ ）
A、2 B、 C、 D、2二、填空题
-
13. 直线l1的斜率为2，l1∥l2 ， 直线l2过点（﹣1，1）且与y轴交于点P，则P点坐标为14. 正三棱台的上、下底面边长及高分别为1，2，2，则它的斜高是15. 一个画家有14个边长为1m的正方体，他在地面上把它摆成如图所示的形式，然后，他把露出的表面都染上颜色，那么被染上颜色的面积为 m2 ．
16. 已知点A（﹣2，0），B（4，0），圆C：（x+4）2+（y+b）2=16，点P是圆C上任意一点，若 为定值，则b= ．三、解答题
-
17. 求经过点A（3，2）圆心在直线y=2x上，与直线y=2x+5相切的圆的方程．18. 如图，在三棱锥P﹣ABC中，平面PAC⊥平面ABC，PA⊥AC，AB⊥BC．设D，E分别为PA，AC中点．
（Ⅰ）求证：DE∥平面PBC；
（Ⅱ）求证：BC⊥平面PAB；
（Ⅲ）试问在线段AB上是否存在点F，使得过三点 D，E，F的平面内的任一条直线都与平面PBC平行？若存在，指出点F的位置并证明；若不存在，请说明理由．
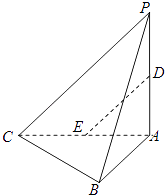19. 如图，在平面直角坐标系xOy中，A（a，0）（a＞0），B（0，a），C（﹣4，0），D（0，4）设△AOB的外接圆圆心为E．
(1)、若⊙E与直线CD相切，求实数a的值；(2)、设点P在圆E上，使△PCD的面积等于12的点P有且只有三个，试问这样的⊙E是否存在，若存在，求出⊙E的标准方程；若不存在，说明理由．20. 如图，三棱柱ABC﹣A1B1C1中，AB=AC=AA1=BC1=2，∠AA1C1=60°，平面ABC1⊥平面AA1C1C，AC1与A1C相交于点D．
(1)、求证：BD⊥A1C；(2)、若E在棱BC1上，且满足DE∥面ABC，求三棱锥E﹣ACC1的体积．
