2016-2017学年贵州省遵义市高三上学期期中数学试卷（理科）

试卷更新日期：2016-12-28 类型：期中考试

进入出卷网下载

一、选择题

1. 已知集合A={x|﹣3＜x＜6}，B={x|2＜x＜7}，则A∩（∁_RB）=（）

A、（2，6） B、（2，7） C、（﹣3，2] D、（﹣3，2）

查看试题解析
2. 已知复数z=a+i，若z+ $\bar{z}$ =4，则复数z的共轭复数 $\bar{z}$ =（）

A、2+i B、2﹣i C、﹣2+i D、﹣2﹣i

查看试题解析
3. 某年级有1000名学生，随机编号为0001，0002，…，1000，现用系统抽样方法，从中抽出200人，若0122号被抽到了，则下列编号也被抽到的是（）

A、0116 B、0927 C、0834 D、0726

查看试题解析
4. 下列四个函数中，在定义域上不是单调函数的是（）

A、y=﹣2x+1 B、y= $\frac{1}{x}$ C、y=lgx D、y=x³

查看试题解析
5. 已知倾斜角为α的直线l过x轴上一点A（非坐标原点O），直线l上有一点P（cos130°，sin50°），且∠APO=30°，则α等于（）

A、100° B、160° C、100°或160° D、130°

查看试题解析
6. 已知 $\frac{1}{a} ＜ \frac{1}{b} ＜ 0$ ，给出下列四个结论：
①a＜b
②a+b＜ab
③|a|＞|b|
④ab＜b²
其中正确结论的序号是（）

A、①② B、②④ C、②③ D、③④

查看试题解析
7. 某几何体的三视图如图所示，则该几何体的表面积为（）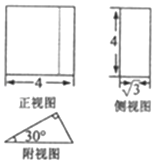

A、 $24 + 12 \sqrt{3}$ B、 $24 + 5 \sqrt{3}$ C、 $12 + 15 \sqrt{3}$ D、 $12 + 12 \sqrt{3}$

查看试题解析
8. 某企业为节能减排，用9万元购进一台新设备用于生产，第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加3万元，该设备每年生产的收入均为21万元，设该设备使用了n（n∈N*）年后，盈利总额达到最大值（盈利额等于收入减去成本），则n等于（）

A、6 B、7 C、8 D、7或8

查看试题解析
9. 如果执行如图所示的程序框图，输入正整数N（N≥2）和实数a₁ ， a₂ ， …，a_n ，输出A，B，则（）

A、A和B分别是a₁ ， a₂ ， …，a_n中最小的数和最大的数 B、A和B分别是a₁ ， a₂ ， …，a_n中最大的数和最小的数 C、 $\frac{A + B}{2}$ 为a₁ ， a₂ ， …，a_n的算术平均数 D、A+B为a₁ ， a₂ ， …，a_n的和

查看试题解析
10. 2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图）．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么sin2θ的值为（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{23}{24}$ D、 $\frac{24}{25}$

查看试题解析
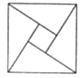11. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的离心率为 $\frac{\sqrt{6}}{2}$ ，左顶点到一条渐近线的距离为 $\frac{2 \sqrt{6}}{3}$ ，则该双曲线的标准方程为（）

A、 $\frac{x^{2}}{12} - \frac{y^{2}}{8} = 1$ B、 $\frac{x^{2}}{16} - \frac{y^{2}}{8} = 1$ C、 $\frac{x^{2}}{16} - \frac{y^{2}}{12} = 1$ D、 $\frac{x^{2}}{8} - \frac{y^{2}}{4} = 1$

查看试题解析
12. 已知定义域为R的偶函数f（x），其导函数为f'（x），对任意x∈[0，+∞），均满足：xf'（x）＞﹣2f（x）．若g（x）=x²f（x），则不等式g（2x）＜g（1﹣x）的解集是（）

A、（﹣∞，﹣1） B、 $(- \infty ， \frac{1}{3})$ C、 $(- 1 ， \frac{1}{3})$ D、 $(- \infty ， - 1) \cup (\frac{1}{3} ， + \infty)$

查看试题解析

二、填空题

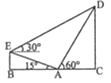
13. 已知x，y满足 ${\begin{matrix} x - 3 \geq 0 \\ y - x \leq 0 \\ x + y - 3 \geq 0 \end{matrix}$ ，则目标函数z=﹣2x+y的最大值为．

查看试题解析
14. （x+ $\frac{a}{x}$ ）（2x﹣ $\frac{1}{x}$ ）⁵的展开式中各项系数的和为2，则该展开式中常数项为．

查看试题解析
15. 某中学举行升旗仪式，在坡度为15°的看台E点和看台的坡脚A点，分别测得旗杆顶部的仰角分别为30°和60°，量的看台坡脚A点到E点在水平线上的射影B点的距离为10cm，则旗杆的高CD的长是 m．

查看试题解析
16. 已知平面α截一球面得圆M，过圆M的圆心的平面β与平面α所成二面角的大小为60°，平面β截该球面得圆N，若该球的表面积为64π，圆M的面积为4π，则圆N的半径为．

查看试题解析

三、解答题

17. 在公差不为零的等差数列{a_n}中，已知a₂=3，且a₁、a₃、a₇成等比数列．

(1)、求数列{a_n}的通项公式；

(2)、设数列{a_n}的前n项和为S_n ，记b_n= $\frac{9}{2 S_{3 n}}$ ，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 2016年巴西奥运会的周边商品有80%左右为“中国制造”，所有的厂家都是经过层层筛选才能获此殊荣．甲、乙两厂生产同一产品，为了解甲、乙两厂的产品质量，以确定这一产品最终的供货商，采用分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件，测量产品中的微量元素的含量（单位：毫克）．下表是从乙厂抽取的5件产品的测量数据：
编号
1
2
3
4
5
x
169
178
166
175
180
y
75
80
77
70
81

(1)、求乙厂生产的产品数量：

(2)、当产品中的微量元素x、y满足：x≥175，且y≥75时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量：

(3)、从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数的分布列及数学期望．

查看试题解析
19. 如图，在直三棱柱ABC﹣A₁B₁C₁中，平面A₁BC⊥侧面A₁ABB₁ ，且AA₁=AB=2．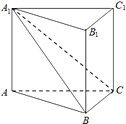

(1)、求证：AB⊥BC；

(2)、若直线AC与平面A₁BC所成的角为 $\frac{π}{6}$ ，求锐二面角A﹣A₁C﹣B的大小．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0），离心率为 $\frac{\sqrt{3}}{2}$ ，两焦点分别为F₁、F₂ ，过F₁的直线交椭圆C于M，N两点，且△F₂MN的周长为8．

(1)、求椭圆C的方程；

(2)、过点P（m，0）作圆x²+y²=1的切线l交椭圆C于A，B两点，求弦长|AB|的最大值．

查看试题解析
21. 已知函数f（x）= $\frac{1 - x}{e^{x}}$ ．

(1)、求曲线y=f（x）在点（0，f（0））处的切线方程和函数f（x）的极值：

(2)、若对任意x₁ ， x₂∈[a，+∞），都有f（x₁）﹣f（x₂）≥﹣ $\frac{1}{e^{2}}$ 成立，求实数a的最小值．

查看试题解析

四、选做题

22. （在平面直角坐标系xOy中，已知曲线C₁：x²+y²=1，以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ（2cosθ﹣sinθ）=6．

(1)、将曲线C₁上的所有点的横坐标、纵坐标分别伸长为原来的 $\sqrt{3}$ 、2倍后得到曲线C₂ ，试写出直线l的直角坐标方程和曲线C₂的参数方程；

(2)、在曲线C₂上求一点P，使点P到直线l的距离最大，并求出此最大值．

查看试题解析
23. 已知∃x₀∈R使得关于x的不等式|x﹣1|﹣|x﹣2|≥t成立．

(1)、求满足条件的实数t集合T；

(2)、若m＞1，n＞1，且对于∀t∈T，不等式log₃m•log₃n≥t恒成立，试求m+n的最小值．

查看试题解析

编号	1	2	3	4	5
x	169	178	166	175	180
y	75	80	77	70	81