2017-2018学年数学沪科版七年级下册8.3.1平方差公式 同步练习
试卷更新日期：2018-05-25 类型：同步测试
一、选择题
-
1. 化简：(a+1)2-(a-1)2=（ ）A、2 B、4 C、4a D、2a2+22. 若M(3x-y2)＝y4-9 x2 ， 则代数式M应是（ ）
A、-(3 x+y2) B、y2-3x C、3x+ y2 D、3 x- y23. 下列多项式中，与-x-y相乘的结果是x2-y2的多项式是（ ）A、y-x B、x-y C、x+y D、-x-y4. 计算：a2-(a+1)(a-1)的结果是（ ）A、1 B、-1 C、2a2+1 D、2a2-15. 若|x+y-5|+(x-y-3)2=0，则x2-y2的结果是（ ）A、2 B、8 C、15 D、无法确定6. 下列因式分解正确的是（ ）A、(x-3)2-y2=x2-6x+9-y2 B、a2-9b2=(a+9b)(a-9b) C、4x6-1=(2x3+1)(2x3-1) D、-x2-y2=(x-y)(x+y)7. 计算(a4+b4)(a2+b2)(b-a)(a+b)的结果是（ ）A、a8-b8 B、a6-b6 C、b8-a8 D、b6-a68. 如图，阴影部分是边长为a的大正方形剪去一个边长为b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列4幅图割拼方法中，其中能够验证平方差公式有（ ）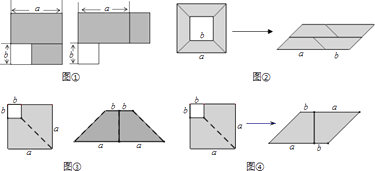
A、①②③④ B、③④ C、①② D、①②③二、填空题
-
9. 如果x+y=-4，x-y=8，那么代数式x2-y2的值是10. （a+1）(a-1)(1-a2)=
11. (x-y+z)()＝z2-( x-y)2 ．12. 若x2-y2=48，x+y=6，则3x-3y=13. 观察下列各式：(a-1)(a+1)=a2-1，(a-1)(a2+a+1)=a3-1，(a-1)(a3+a2+a+1)=a4-1…根据前面各式的规律计算：(a-1)(a4+a3+a2+a+1)= ；22012+22011+…+22+2+1= ．
14. 一个自然数若能表示为两个自然数的平方差，则这个自然数称为“智慧数”．比如：22-12=3，则3就是智慧数；22-02=4，则4就是智慧数．从0开始第7个智慧数是 ；不大于200的智慧数共有 ．
三、计算题
-
15. 先化简，再求值．(a2 b-2 ab2- b3)÷b-( a+b)(a-b)，其中a＝ ，b＝-1．16. 化简
(1)、( x- y)( x+ y) ( x2+ y2) ( x4+ y4)·…·(x16+ y16)；(2)、(22+1)(24+1)(28+1)(216+1)．17. 如图1，从边长为a的正方形纸片中剪去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸片拼成如图2的等腰梯形.
(1)、设图1中阴影部分面积为S1 ， 图2中阴影部分面积为S2 ， 请直接用含a，b的代数式表示S1 ， S2.(2)、请写出上述过程所揭示的乘法公式.18. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘 数”．如：4＝22-02 ， 12＝42-22 ， 20＝62-42 ， 因此4，12，20这三个数都是神秘数．(1)、28和2012这两个数是神秘数吗?为什么?(2)、设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗?为什么?(3)、两个连续奇数的平方差(取正数)是神秘数吗?为什么?19. 老师在黑板上写出三个算式：52－32＝8×2，92－72＝8×4，152－32＝8×27，王华接着又写了两个具有同样规律的算式：112－52＝8×12，152－72＝8×22，…(1)、请你再写出两个(不同于上面算式)具有上述规律的算式；(2)、用文字写出反映上述算式的规律；(3)、证明这个规律的正确性．