安徽省淮南市西部地区2018届数学中考五模试卷

试卷更新日期：2018-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 已知是等腰直角三角形的一个锐角，则的值为（）

A、 B、 $\frac{\sqrt{2}}{2}$ C、 D、1

查看试题解析
2. 右面的三视图对应的物体是（）

A、 B、 C、 D、

查看试题解析
3. 在△ABC中，∠C=90°，AB=6，cosA= $\frac{1}{3}$ ，则AC等于（）.

A、18 B、2 C、 $\frac{1}{2}$ D、 $\frac{1}{18}$

查看试题解析
4. 如图是一个由5个相同的正方体组成的立体图形，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，滑雪场有一坡角α为20°的滑雪道，滑雪道AC的长为200米，则滑雪道的坡顶到坡底垂直高度AB的长为（）

A、200tan20°米 B、 $\frac{200}{sin 20^{\circ}}$ 米 C、200sin20°米 D、200cos20°米

查看试题解析
6. 如图，上下底面为全等的正六边形礼盒，其正视图与侧视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（）

A、320cm B、395.24cm C、431.77cm D、480cm

查看试题解析
7. 在下列网格中，小正方形的边长为1，点A，B，O都在格点上，则∠A的正弦值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{10}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，在半径为5的⊙O中，弦AB=6，点C是优弧 $\overset{⌢}{A B}$ 上一点（不与A，B重合），则cosC的值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 如图，在△ABC中，∠ACB=90°，AC=BC=4，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE=3，则sin∠BFD的值为（）

A、 $\frac{1}{3}$ B、 $\frac{2 \sqrt{2}}{3}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{3}{5}$

查看试题解析
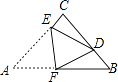10. 如图，四边形ABCD，A₁B₁BA，…，A₅B₅B₄A₄都是边长为1的小正方形．已知∠ACB=a，∠A₁CB₁=a₁ ， …，∠A₅CB₅=a₅ ．则tana•tana₁+tana₁•tana₂+…+tana₄•tana₅的值为（）

A、 $\frac{5}{6}$ B、 $\frac{4}{5}$ C、1 D、 $\sqrt{5}$

查看试题解析

二、填空题

11. 已知∠A是锐角，且tanA= $\frac{\sqrt{3}}{3}$ ，则∠A= ．

查看试题解析
12. 坡角为α=60°，则坡度i= ．

查看试题解析
13. 如图，一个几何体的三视图分别是两个矩形、一个扇形，则这个几何体表面积的大小为．

查看试题解析
14. 如图，一根木棒（AB）长为2a，斜靠在与地面（OM）垂直的墙壁（ON）上，与地面的倾斜角（∠ABO）为60°，当木棒A端沿N0向下滑动到A′，AA′=（ $\sqrt{3} - \sqrt{2}$ ）a，B端沿直线OM向右滑动到B′，则木棒中点从P随之运动到P′所经过的路径长为．

查看试题解析

三、解答题

15. 计算：2cos45°﹣tan60°+sin30°﹣|﹣ $\frac{1}{2}$ |．

查看试题解析
16. 如图是某工件的三视图，求此工件的全面积和体积．

查看试题解析
17. 在平面直角坐标系中，若△ABC的三个顶点的坐标分别为A（﹣4，1），B（﹣1，3），C（﹣4，3），求sinB的值．

查看试题解析
18. 如图，在△ABC中，∠A=30°，cosB= $\frac{4}{5}$ ，AC= $6 \sqrt{3}$ .求AB的长.

查看试题解析
19. 一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长．

查看试题解析
20. 已知：α为锐角，关于x的一元二次方程3x²﹣2 $\sqrt{3}$ x+tanα=0有两个相等的实数根．

(1)、求锐角α；

(2)、求方程的根．

查看试题解析
21. 如图，是住宅区内的两幢楼，它们的高AB=CD=30m，两楼间的距离AC=30m，现需了解甲楼对乙楼的采光的影响情况．

(1)、当太阳光与水平线的夹角为30°角时，求甲楼的影子在乙楼上有多高（精确到0.1m， $\sqrt{3}$ =1.73）；

(2)、若要甲楼的影子刚好不落在乙楼的墙上，此时太阳与水平线的夹角为多少度？

查看试题解析
22. 如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向，测绘员沿主输气管道步行1000米到达C处，测得小区M位于点C的北偏西75°方向，试在主输气管道AC上寻找支管道连接点N，使其到该小区铺设的管道最短，并求AN的长．（精确到1米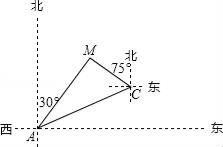， $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
23. 在直角三角形ABC中，∠ABC=90°，∠C=30°，AB=4，以B为圆心，BA为半径作⊙B交BC于点D，旋转∠ABD交⊙B于点E、F，连接EF交AC、BC边于点G、H．

(1)、若BE⊥AC，求tan∠CGH的值；

(2)、若AG=4，求△BEF与△ABC重叠部分的面积；

(3)、△BHE是等腰三角形时，∠ABD逆时针旋转的度数是．

查看试题解析