2018年浙江省义乌市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-24 类型:中考模拟
一、选择题
-
1. ﹣5的相反数是( )A、5 B、±5 C、﹣5 D、2. 下面长方体的主视图(主视图也称正视图)是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 端午节前夕,某超市用1680元购进A、B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )A、 B、 C、 D、4. 下列调查方式中适合的是( )A、要了解一批节能灯的使用寿命,采用普查方式 B、调查你所在班级同学的身高,采用抽样调查方式 C、环保部门调查沱江某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用普查方式5. 如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )
3. 端午节前夕,某超市用1680元购进A、B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )A、 B、 C、 D、4. 下列调查方式中适合的是( )A、要了解一批节能灯的使用寿命,采用普查方式 B、调查你所在班级同学的身高,采用抽样调查方式 C、环保部门调查沱江某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用普查方式5. 如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( ) A、4+4﹣ =6 B、4+40+40=6 C、4+ =6 D、4﹣1÷ +4=66. 对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A、4+4﹣ =6 B、4+40+40=6 C、4+ =6 D、4﹣1÷ +4=66. 对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A、某市明天将有75%的时间下雨 B、某市明天将有75%的地区下雨 C、某市明天一定下雨 D、某市明天下雨的可能性较大7. 已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )A、8 B、9 C、10 D、118. 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )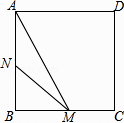 A、
A、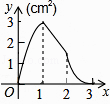 B、
B、 C、
C、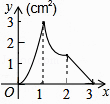 D、
D、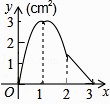 9. 如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
9. 如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( ) A、
A、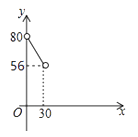 B、
B、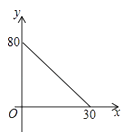 C、
C、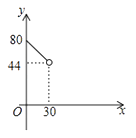 D、
D、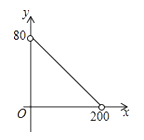 10. 如图所示,已知:y=(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为0,b)(b>0).
10. 如图所示,已知:y=(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2 , 此时P点的坐标为( )
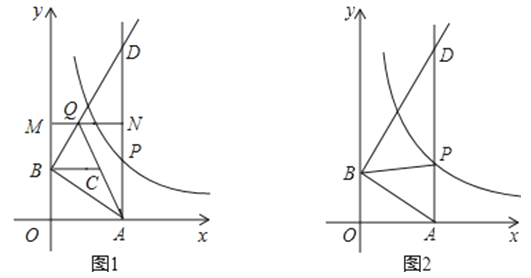 A、(3,2) B、( , 3) C、(4,) D、( , )
A、(3,2) B、( , 3) C、(4,) D、( , )二、填空题
-
11. 分解因式:x2y﹣2xy2+y3= .12. 某校2013(3)班的四个小组中,每个小组同学的平均身高大致相同,若:
第一小组同学身高的方差为1.7,第二小组同学身高的方差为1.9,
第三小组同学身高的方差为2.3,第四小组同学身高的方差为2.0,
则在这四个小组中身高最整齐的是第小组.
13.不等式组
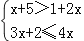 的解集是 . 14. 如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将▱ABCO绕点A逆时针旋转得到▱ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数y= (x<0)的图象上,则k的值为
的解集是 . 14. 如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将▱ABCO绕点A逆时针旋转得到▱ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数y= (x<0)的图象上,则k的值为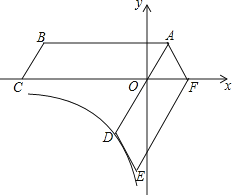
15. 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为 .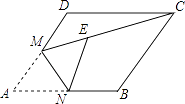 16.
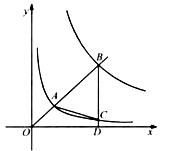
16.如图,在平面直角坐标系 中,已知直线 ( )分别交反比例函数 和 在第一象限的图象于点 , ,过点 作 轴于点 ,交 的图象于点 ,连结 .若 是等腰三角形,则 的值是 .
三、解答题
-
17. 先化简,再求值(x﹣2)2+2(x+2)(x+4)﹣(x﹣3)(x+3);其中x=﹣1.18. 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
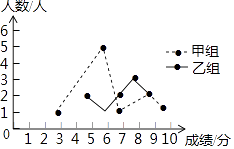 (1)、求出下列成绩统计分析表中a,b的值:
(1)、求出下列成绩统计分析表中a,b的值:组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)、小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.19. 如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.
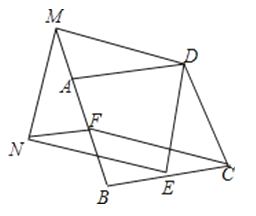 20.
20.如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
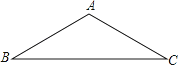 21. 如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
21. 如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)、通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm
0
1
2
3
4
5
6
y/cm
0
2.0
2.3
2.1
0.9
0
(说明:补全表格时相关数值保留一位小数)
(2)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象. (3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.22. 某中学开学初到商场购买A、B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,已知购买一个B种品牌的足球比购买一个A钟品牌的足球多花30元.(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元.(2)、学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?(3)、请你求出学校在第二次购买活动中最多需要多少资金?23. 如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线 与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.22. 某中学开学初到商场购买A、B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,已知购买一个B种品牌的足球比购买一个A钟品牌的足球多花30元.(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元.(2)、学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?(3)、请你求出学校在第二次购买活动中最多需要多少资金?23. 如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线 与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.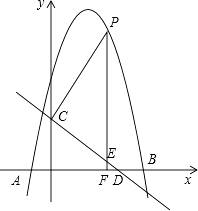 (1)、求抛物线的解析式;(2)、若PE=5EF,求m的值;(3)、若点E′ 是点E关于直线PC的对称点(E与C不重合),是否存在点P,使点E′ 落在y轴上?若存在,请求出相应的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若PE=5EF,求m的值;(3)、若点E′ 是点E关于直线PC的对称点(E与C不重合),是否存在点P,使点E′ 落在y轴上?若存在,请求出相应的点P的坐标;若不存在,请说明理由.
24. 我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D﹣d.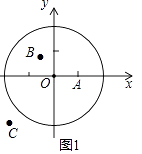 (1)、①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
(1)、①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:A(1,0)的距离跨度;
B(﹣ , )的距离跨度;
C(﹣3,﹣2)的距离跨度;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 .
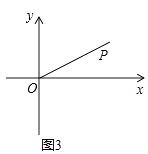
(2)、如图2,在平面直角坐标系xOy中,图形G2为以D(﹣1,0)为圆心,2为半径的圆,直线y=k(x﹣1)上存在到G2的距离跨度为2的点,求k的取值范围.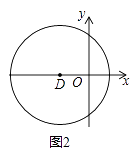 (3)、如图3,在平面直角坐标系xOy中,射线OP:y= x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,直接写出圆心E的横坐标xE的取值范围 .
(3)、如图3,在平面直角坐标系xOy中,射线OP:y= x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,直接写出圆心E的横坐标xE的取值范围 .