2018年浙江省温州市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-24 类型:中考模拟
一、选择题
-
1. 下列各组数中,互为相反数的是( )A、﹣1与(﹣1)2 B、1与(﹣1)2 C、2与 D、2与|﹣2|2. 某校对学生上学方式进行了一次抽样调查,如图是根据此次调查结果所绘制的一个未完成的扇形统计图,已知该校学生共有2560人,被调查的学生中骑车的有21人,则下列四种说法中,不正确的是( )
 A、被调查的学生有60人 B、被调查的学生中,步行的有27人 C、估计全校骑车上学的学生有1152人 D、扇形图中,乘车部分所对应的圆心角为54°3. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、
A、被调查的学生有60人 B、被调查的学生中,步行的有27人 C、估计全校骑车上学的学生有1152人 D、扇形图中,乘车部分所对应的圆心角为54°3. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、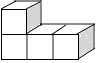 B、
B、 C、
C、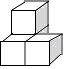 D、
D、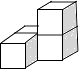 4. 设的小数部分为b,那么(4+b)b的值是( )A、1 B、是一个有理数 C、3 D、无法确定5. 某超市购进了一批不同价格的皮鞋,下表是该超市在近几年统计的平均数据,要使该超市销售皮鞋收入最大,该超市应多购哪种价位的皮鞋( )
4. 设的小数部分为b,那么(4+b)b的值是( )A、1 B、是一个有理数 C、3 D、无法确定5. 某超市购进了一批不同价格的皮鞋,下表是该超市在近几年统计的平均数据,要使该超市销售皮鞋收入最大,该超市应多购哪种价位的皮鞋( )皮鞋价(元)
160
140
120
100
销售百分率
60%
75%
83%
95%
A、160元 B、140元 C、120元 D、100元6. 若一次函数y=(1﹣2m)x+m的图象经过点A(x1 , y1)和点B(x2 , y2),当x1<x2时,y1<y2 , 且与y轴相交于正半轴,则 m的取值范围是( )A、m>0 B、m< C、0<m< D、m>7. 如图,将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6cm(如箭头所示),则木桩上升了( )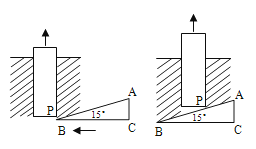 A、6sin15°cm B、6cos15°cm C、6tan15°cm D、 cm8. 若x=1是方程ax2+bx+c=0的解,则( )A、a+b+c=1 B、a-b+c=0 C、a+b+c=0 D、a-b-c=09. 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为( )
A、6sin15°cm B、6cos15°cm C、6tan15°cm D、 cm8. 若x=1是方程ax2+bx+c=0的解,则( )A、a+b+c=1 B、a-b+c=0 C、a+b+c=0 D、a-b-c=09. 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为( )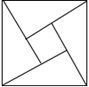 A、49 B、25 C、13 D、110.
A、49 B、25 C、13 D、110.在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定;正方形内部不包括边界上的点,如果如图所示的中心在原点,一边平行于x轴的正方形,边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整数点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内的整点个数为( )
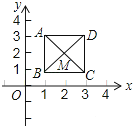 A、42 B、40 C、36 D、49
A、42 B、40 C、36 D、49二、填空题
-
11. 把多项式x3﹣9x分解因式的结果是 .12. 一组数据﹣1,x,0,5,3,﹣2的平均数是1,则这组数据的中位数是 .13. 如图,在△ABC中,以边AB上的一点O为圆心,以OA的长为半径的圆交边AB于点D,BC与⊙O相切于点C.若⊙O的半径为5,∠A=20°,则 的长为 .
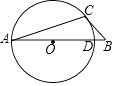 14. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意列方程为 .15. 如图,已知点A是双曲线y= 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y= 上运动,则k的值是 .
14. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意列方程为 .15. 如图,已知点A是双曲线y= 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y= 上运动,则k的值是 .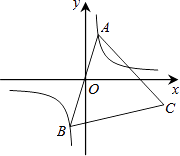 16. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.
16. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.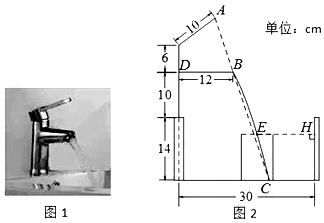
三、解答题
-
17. ①计算|﹣2|+( )0+2sin30°﹣( )﹣1
②先化简,再求值:(a+ )÷ ,其中a=1﹣ .
18. 如图1,我们把对角线互相垂直的四边形叫做垂美四边形.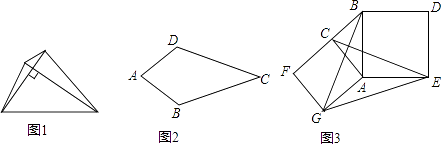 (1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.(2)、性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
(1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.(2)、性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.猜想结论:(要求用文字语言叙
写出证明过程(先画出图形,写出已知、求证).
(3)、问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.19. 为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).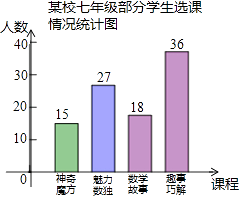 (1)、学校对七年级部分学生进行选课调查,得到如图所示的统计图.根据该统计图,请估计该校七年级480名学生选“数学故事”的人数.(2)、学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)20. 如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F.(1)、如图1,求证:DE=DF;
(1)、学校对七年级部分学生进行选课调查,得到如图所示的统计图.根据该统计图,请估计该校七年级480名学生选“数学故事”的人数.(2)、学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)20. 如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F.(1)、如图1,求证:DE=DF; (2)、如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点;
(2)、如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点; (3)、如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG= ,AB=3,求线段BH的长
(3)、如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG= ,AB=3,求线段BH的长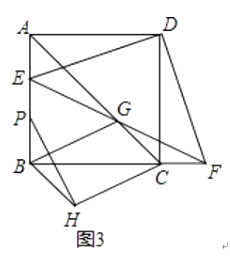 21. 如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.
21. 如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.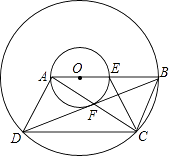 22. 在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).
22. 在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧). (1)、求该抛物线的表达式及点B,C的坐标;(2)、抛物线的对称轴与x轴交于点D,若直线y=kx+b经过点D和点E(﹣1,﹣2),求直线DE的表达式;(3)、在(2)的条件下,已知点P(t,0),过点P作垂直于x轴的直线交抛物线于点M,交直线DE于点N,若点M和点N中至少有一个点在x轴下方,直接写出t的取值范围.23. 为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
(1)、求该抛物线的表达式及点B,C的坐标;(2)、抛物线的对称轴与x轴交于点D,若直线y=kx+b经过点D和点E(﹣1,﹣2),求直线DE的表达式;(3)、在(2)的条件下,已知点P(t,0),过点P作垂直于x轴的直线交抛物线于点M,交直线DE于点N,若点M和点N中至少有一个点在x轴下方,直接写出t的取值范围.23. 为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
220
180
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)、求a,b的值;(2)、经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;(3)、在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.24. 在平面直角坐标系中,点Q为坐标系上任意一点,某图形上的所有点在∠Q的内部(含角的边),这时我们把∠Q的最小角叫做该图形的视角.如图1,矩形ABCD,作射线OA,OB,则称∠AOB为矩形ABCD的视角. (1)、如图1,矩形ABCD,A(﹣ ,1),B( ,1),C( ,3),D(﹣ ,3),直接写出视角∠AOB的度数;
(1)、如图1,矩形ABCD,A(﹣ ,1),B( ,1),C( ,3),D(﹣ ,3),直接写出视角∠AOB的度数; (2)、在(1)的条件下,在射线CB上有一点Q,使得矩形ABCD的视角∠AQB=60°,求点Q的坐标;(3)、如图2,⊙P的半径为1,点P(1, ),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.
(2)、在(1)的条件下,在射线CB上有一点Q,使得矩形ABCD的视角∠AQB=60°,求点Q的坐标;(3)、如图2,⊙P的半径为1,点P(1, ),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.