2018年浙江省绍兴市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-24 类型:中考模拟
一、选择题
-
1. 计算(﹣1)2017的结果是( )A、﹣1 B、1 C、﹣2017 D、20172. H7N9型禽流感是一种新型禽流感,于2013年3月底在上海和安徽两地率先发现.H7N9型禽流感是全球首次发现的新亚型流感病毒,其细胞的直径约为0.000000106m,用科学记数法表示这个数是( )A、0.106×10﹣6m B、0.106×106m C、1.06×10﹣7m D、1.06×107m3.
如图,是一个几何体的三视图,根据图中标注的数据可求得这个几何体的体积为( )
 A、24π B、32π C、36π D、48π4. 一个不透明的袋子装有3个小球,它们除分别标有的数字1,3,5不同外,其他完全相同,任意从袋子中摸出一球后放回,再任意摸出一球,则两次摸出的球所标数字之和为6的概率是( )A、 B、 C、 D、5. 某次体育测试后,12名九年级学生的成绩如下表所示,这这组数据的众数和中位数分别是( )
A、24π B、32π C、36π D、48π4. 一个不透明的袋子装有3个小球,它们除分别标有的数字1,3,5不同外,其他完全相同,任意从袋子中摸出一球后放回,再任意摸出一球,则两次摸出的球所标数字之和为6的概率是( )A、 B、 C、 D、5. 某次体育测试后,12名九年级学生的成绩如下表所示,这这组数据的众数和中位数分别是( )成绩
68
67
69.5
70
69
人数
2
1
2
3
4
A、69,69.5 B、70,69 C、69,69 D、69,706.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
 A、8米 B、10米 C、12米 D、14米7.
A、8米 B、10米 C、12米 D、14米7.如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
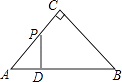 A、
A、 B、
B、 C、
C、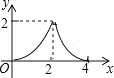 D、
D、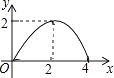 8. 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
8. 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( ) A、75° B、60° C、55° D、45°9. 坐标平面上,若移动二次函数y=-(x-2016)(x-2017)+2的图象,使其与 x轴交于两点, 且此两点的距离为1个单位,则移动方式可为( )A、向上平移2个单位 B、向下平移2个单位 C、向上平移1个单位 D、向下平移 1 个单位10. 在由相同的小正方形组成的3×4的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形构成的图形为轴对称图形,则涂下列哪些正方形是正确的( )
A、75° B、60° C、55° D、45°9. 坐标平面上,若移动二次函数y=-(x-2016)(x-2017)+2的图象,使其与 x轴交于两点, 且此两点的距离为1个单位,则移动方式可为( )A、向上平移2个单位 B、向下平移2个单位 C、向上平移1个单位 D、向下平移 1 个单位10. 在由相同的小正方形组成的3×4的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形构成的图形为轴对称图形,则涂下列哪些正方形是正确的( )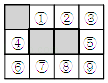 A、①或② B、③或⑥ C、④或⑤ D、③或⑨11. 下图所示的实验操作不正确的是( )A、
A、①或② B、③或⑥ C、④或⑤ D、③或⑨11. 下图所示的实验操作不正确的是( )A、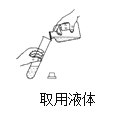 B、
B、 C、
C、 D、
D、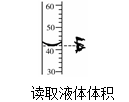
二、填空题
-
12. 分解因式:x3﹣x2﹣20x= .13. 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为;∠A的度数为 .
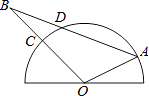 14. 如图,点A为函数y= (x>0)图象上一点,连结OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
14. 如图,点A为函数y= (x>0)图象上一点,连结OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 15. 正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于F,则EF的长为 .
15. 正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于F,则EF的长为 .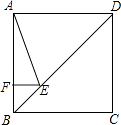 16.
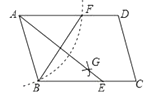
16.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为 .
 17. 如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
17. 如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.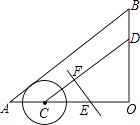
三、解答题
-
18. (1)计算: , (2)求不等式组的整数解.19. 钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
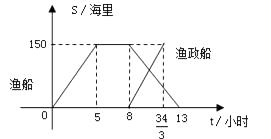 (1)、直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.
(1)、直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.
(2)、求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)、在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
20. 某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: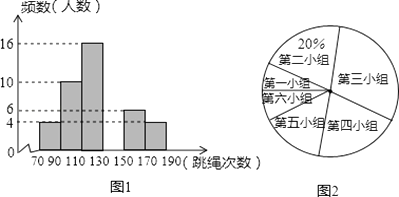 (1)、补全频数分布直方图 , 并指出这个样本数据的中位数落在第小组;(1)
(1)、补全频数分布直方图 , 并指出这个样本数据的中位数落在第小组;(1)
(2)、若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)、如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
21. 如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).求: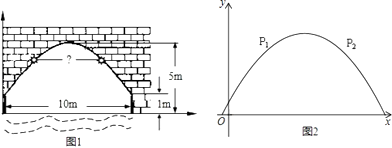 (1)、抛物线的解析式;(2)、两盏景观灯P1、P2之间的水平距离.22. 如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)、抛物线的解析式;(2)、两盏景观灯P1、P2之间的水平距离.22. 如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.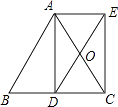 (1)、求证:四边形ADCE的是矩形;(2)、若AB=17,BC=16,求四边形ADCE的面积.23. 如图1(注:与图2完全相同),二次函数y= x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)、求证:四边形ADCE的是矩形;(2)、若AB=17,BC=16,求四边形ADCE的面积.23. 如图1(注:与图2完全相同),二次函数y= x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.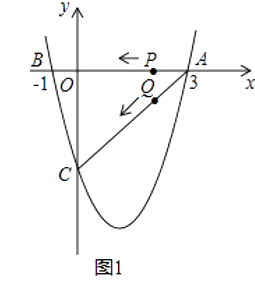
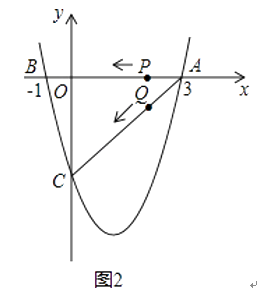 (1)、求该二次函数的解析式;
(1)、求该二次函数的解析式;
(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
24.一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向,B位于南偏西30°方向.
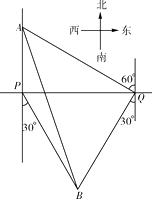 (1)、线段BQ与PQ是否相等?请说明理由;
(1)、线段BQ与PQ是否相等?请说明理由;
(2)、求A、B间的距离(结果保留根号).
25.感知:如图①,点E在正方形ABCD的边BC上,BF⊥AE于点F,DG⊥AE于点G,可知△ADG≌△BAF.(不要求证明)
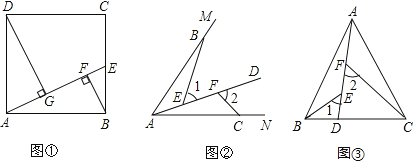 (1)、拓展:如图②,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2= ∠ BAC,求证:△ABE≌△CAF.
(1)、拓展:如图②,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2= ∠ BAC,求证:△ABE≌△CAF.
(2)、应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为 .