2018年浙江省衢州市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-24 类型:中考模拟
一、选择题
-
1. 5的相反数是( )A、 B、﹣5 C、±5 D、﹣2.
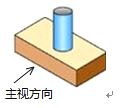
如图所示的几何体是由一个圆柱体和一个长方形组成的,则这个几何体的俯视图是( )
 A、
A、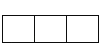
B、
B、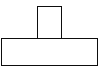
C、
C、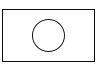
D、
D、
3. 下列计算正确的是( )A、b2•b2=b8 B、x2+x4=x6 C、a3•a3=a9 D、a8•a=a94. “莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
3. 下列计算正确的是( )A、b2•b2=b8 B、x2+x4=x6 C、a3•a3=a9 D、a8•a=a94. “莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:阅读数量
1本
2本
3本
3本以上
人数(人)
10
18
13
4
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A、平均数 B、中位数 C、众数 D、方差5.如图,装修工人向墙上钉木条.若∠2=110°,要使木条b与a平行,则∠1的度数等于( ).
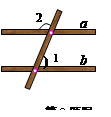 A、55° B、70° C、90° D、110°6. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人.根据题意,列方程组正确的是( )A、 B、 C、 D、7. 如图,小明在作线段AB的垂直平分线时,是这样操作的:分别以点A、B为圆心,大于线段AB长度一半的长为半径画弧,相交于C、D,则直线CD即为所求,连接AC、BC、BD,根据他的作图方法可知,四边形ADBC一定是( )
A、55° B、70° C、90° D、110°6. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人.根据题意,列方程组正确的是( )A、 B、 C、 D、7. 如图,小明在作线段AB的垂直平分线时,是这样操作的:分别以点A、B为圆心,大于线段AB长度一半的长为半径画弧,相交于C、D,则直线CD即为所求,连接AC、BC、BD,根据他的作图方法可知,四边形ADBC一定是( )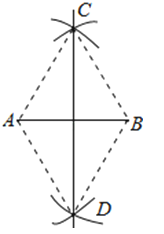 A、矩形 B、菱形 C、正方形 D、梯形8. 如图,直线l和双曲线 (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )
A、矩形 B、菱形 C、正方形 D、梯形8. 如图,直线l和双曲线 (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )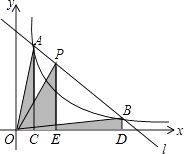 A、S1<S2<S3 B、S1>S2>S3 C、S1=S2>S3 D、S1=S2<S39. 如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ,∠EFA=60°,则四边形A′B′EF的周长是( )
A、S1<S2<S3 B、S1>S2>S3 C、S1=S2>S3 D、S1=S2<S39. 如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ,∠EFA=60°,则四边形A′B′EF的周长是( ) A、1+3 B、3+ C、4+ D、5+10. 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A、1+3 B、3+ C、4+ D、5+10. 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )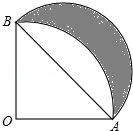
A、 B、 C、 D、二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是 .12. 已知 ,则
13. 如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为 .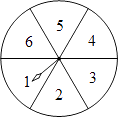 14.
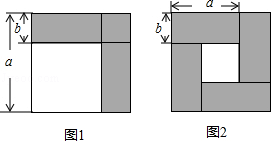
14.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图1可以用来解释a2﹣b2=(a+b)(a﹣b).那么通过图2面积的计算,验证了一个恒等式,此等式是
.
 15.
15.如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).
 (1)、当直线AB经过点C时,点O到直线AB的距离是;(2)、设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.16. 如图,四条直线l1:y1= x,l2:y2= x,l3:y3=﹣ x,l4:y4=﹣ x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2 , 再过点A2作A2A3⊥l1交l2于点A3 , 再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为 .
(1)、当直线AB经过点C时,点O到直线AB的距离是;(2)、设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.16. 如图,四条直线l1:y1= x,l2:y2= x,l3:y3=﹣ x,l4:y4=﹣ x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2 , 再过点A2作A2A3⊥l1交l2于点A3 , 再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为 .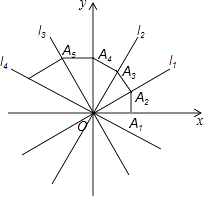
三、解答题
-
17. 计算:( )﹣1+2cos30°﹣| ﹣1|+(﹣1)2017 .18. 解不等式,并把它的解集表示在数轴上:5x﹣2>3(x+1)19. 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;
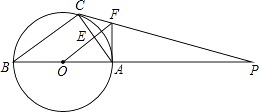 (1)、判断AF与⊙O的位置关系并说明理由.(2)、若⊙O的半径为4,AF=3,求AC的长.20. 2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图:
(1)、判断AF与⊙O的位置关系并说明理由.(2)、若⊙O的半径为4,AF=3,求AC的长.20. 2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图: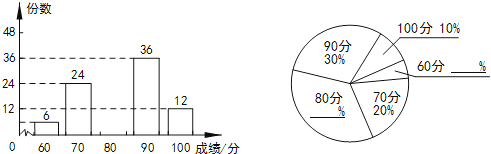
根据以上信息,解答下列问题:
(1)、求本次抽取了多少份作品,并补全两幅统计图;(2)、已知该校收到参赛作品共900份,比赛成绩达到90分以上(含90分)的为优秀作品,据此估计该校参赛作品中,优秀作品有多少份?
21. 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线 过点A(—1,0),与⊙C相切于点D, (1)、求∠CAD的度数。(2)、求直线 的解析式。22. 设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数 ,当x=1时,y=3;当x=3时,y=1,即当 时,有 ,所以说函数 是闭区间[1,3]上的“闭函数”.(1)、反比例函数y= 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;(2)、若二次函数y= 是闭区间[1,2]上的“闭函数”,求k的值;(3)、若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示).23. 解答题(1)、如图1,在正方形ABCD中,点O是对角线AC的中点,点E是边BC上一点,连接OE,过点O作OE的垂线交AB于点F.求证:OE=OF.
(1)、求∠CAD的度数。(2)、求直线 的解析式。22. 设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数 ,当x=1时,y=3;当x=3时,y=1,即当 时,有 ,所以说函数 是闭区间[1,3]上的“闭函数”.(1)、反比例函数y= 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;(2)、若二次函数y= 是闭区间[1,2]上的“闭函数”,求k的值;(3)、若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示).23. 解答题(1)、如图1,在正方形ABCD中,点O是对角线AC的中点,点E是边BC上一点,连接OE,过点O作OE的垂线交AB于点F.求证:OE=OF.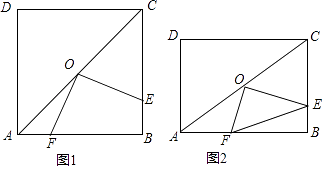 (2)、若将(1)中,“正方形ABCD”改为“矩形ABCD”,其他条件不变,如图2,连接EF.
(2)、若将(1)中,“正方形ABCD”改为“矩形ABCD”,其他条件不变,如图2,连接EF.ⅰ)求证:∠OEF=∠BAC.
ⅱ)试探究线段AF,EF,CE之间数量上满足的关系,并说明理由.
24. 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s). (1)、若m=6,求当P,E,B三点在同一直线上时对应的t的值.(2)、已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
(1)、若m=6,求当P,E,B三点在同一直线上时对应的t的值.(2)、已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.