2018年浙江省宁波市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-24 类型:中考模拟
一、选择题
-
1. ﹣8的绝对值等于( )A、8 B、﹣8 C、 D、2. 下列运算中,正确的是( )A、x3•x3=x6 B、3x2+2x3=5x5 C、(x2)3=x5 D、(ab)3=a3b3. 我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水。据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升。小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后水龙头滴了( )毫升水.(用科学记数法表示,保留两位有效数字)
A、1.4×102 B、1.4×103 C、0.14×104 D、1.44×1034. 为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( )
A、方差 B、众数 C、中位数 D、平均数5. 如图是一个由4个相同的长方体组成的立体图形,它的左视图是( )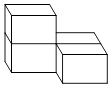 A、
A、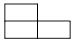 B、
B、 C、
C、 D、
D、 6.
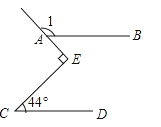
6.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
 A、132° B、134° C、136° D、138°7. 如图,如果▱ABCD的对角线AC,BD相交于点O,那么图中的全等三角形共有( )
A、132° B、134° C、136° D、138°7. 如图,如果▱ABCD的对角线AC,BD相交于点O,那么图中的全等三角形共有( )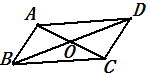 A、1对 B、2对 C、3对 D、4对8. 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A,B,C,若∠BCO=45°,则∠BAC的大小为( )
A、1对 B、2对 C、3对 D、4对8. 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A,B,C,若∠BCO=45°,则∠BAC的大小为( )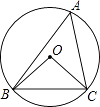 A、22.5° B、35° C、45° D、67.5°9. 如图,在△ABC中,∠C=90°,AC>BC,若以AC为底面圆半径、BC为高的圆锥的侧面积为S1 , 以BC为底面圆半径、AC为高的圆锥的侧面积为S2 , 则( )
A、22.5° B、35° C、45° D、67.5°9. 如图,在△ABC中,∠C=90°,AC>BC,若以AC为底面圆半径、BC为高的圆锥的侧面积为S1 , 以BC为底面圆半径、AC为高的圆锥的侧面积为S2 , 则( ) A、S1 =S2 B、S1>S2 C、S1<S2 D、S1 ,S2的大小大小不能确定10. 如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为( )
A、S1 =S2 B、S1>S2 C、S1<S2 D、S1 ,S2的大小大小不能确定10. 如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为( ) A、1cm2 B、1.5cm2 C、2cm2 D、3cm211. 如图在平面直角坐标系中,抛物线y=(x﹣h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
A、1cm2 B、1.5cm2 C、2cm2 D、3cm211. 如图在平面直角坐标系中,抛物线y=(x﹣h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )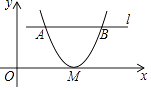 A、 B、 C、2 D、12.
A、 B、 C、2 D、12.在平面直角坐标系中,正方形的顶点坐标分别为 A(1,1),B(1,﹣1),C(﹣1,﹣1),D(﹣1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1 , 作点P1关于点B的对称点P2 , 作点P2关于点C的对称轴P3 , 作点P3关于点D的对称点P4 , 作点P4关于点A的对称点P5 , 作点P5关于点B的对称点P6 , …,按此操作下去,则点P2016的坐标为( )
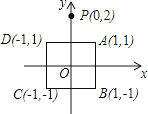 A、(0,2) B、(2,0) C、(0,-2) D、(﹣2,0)
A、(0,2) B、(2,0) C、(0,-2) D、(﹣2,0)二、填空题
-
13. ﹣4是的立方根.14. 因式分解:9x2﹣4= .
15. 写出命题“两直线平行,同位角相等”的结论部分: .16. 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高 m(结果保留根号).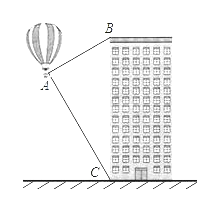 17. 如图,在矩形 中, ,分别以点 、 为圆心, 为半径画弧,与 边分别交于点 、 ,且与对角线 交于同一点 ,则图中阴影部分的面积为 .
17. 如图,在矩形 中, ,分别以点 、 为圆心, 为半径画弧,与 边分别交于点 、 ,且与对角线 交于同一点 ,则图中阴影部分的面积为 .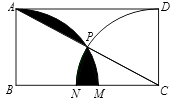 18. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k= .
18. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k= .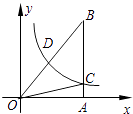
三、解答题
-
19. 解不等式组: ,并在数轴上表示不等式组的解集.20. 甲、乙两人玩“锤子、石头、剪子、布”游戏.他们在不透明的袋子中放入形状、大小均相同的19张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为3、4、5、7,两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
21. 小丽学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图: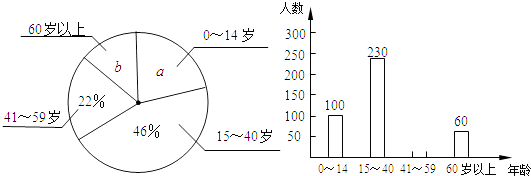
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)、小丽同学共调查了名居民的年龄,扇形统计图中a= , b= , 中位数在年龄段内;(2)、补全条形统计图;(3)、若该辖区年龄在0~14岁的居民约有3500人,请估计年龄在15~59岁的居民的人数.
22. 某市火车站北广场将于2016年底投入使用,计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600 棵.(1)、A,B两种花木的数量分别是多少棵?(2)、如果园林处安排13人同时种植这两种花木,每人每天能种植A花木60棵或B花木40 棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?23. 已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.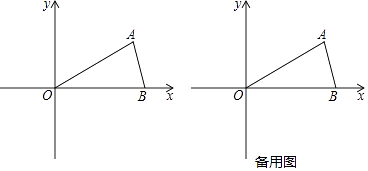 (1)、求点A、B的坐标;(2)、开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;(3)、设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ,P(m,2)(m>0),求m的值.24. 已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.
(1)、求点A、B的坐标;(2)、开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;(3)、设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ,P(m,2)(m>0),求m的值.24. 已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.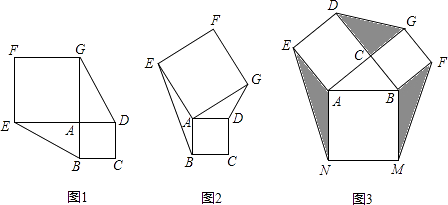 (1)、发现:如图1,当E点旋转到DA的延长线上时,△ABE与△ADG的面积关系是:;(2)、引申:当正方形AEFG旋转任意一个角度时,△ABE与△ADG的面积关系是:;(3)、如图3,四边形ABMN、四边形DEAC、四边形BFGC均为正方形,则S△ABC、S△AEN、S△BMF、S△DCG的关系是;(4)、运用:某小区中有一块空地,要在其中建三个正方形健身场所(如图3),其余空地修成草坪.若已知其中一个正方形的边长为5m,另一个正方形的边长为4m,则草坪的最大面积是 .25. 如图1,已知双曲线y= (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)、发现:如图1,当E点旋转到DA的延长线上时,△ABE与△ADG的面积关系是:;(2)、引申:当正方形AEFG旋转任意一个角度时,△ABE与△ADG的面积关系是:;(3)、如图3,四边形ABMN、四边形DEAC、四边形BFGC均为正方形,则S△ABC、S△AEN、S△BMF、S△DCG的关系是;(4)、运用:某小区中有一块空地,要在其中建三个正方形健身场所(如图3),其余空地修成草坪.若已知其中一个正方形的边长为5m,另一个正方形的边长为4m,则草坪的最大面积是 .25. 如图1,已知双曲线y= (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题: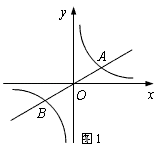 (1)、若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ≤k′x;(2)、如图2,过原点O作另一条直线l,交双曲线y= (k>0)于P,Q两点,点P在第一象限.
(1)、若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ≤k′x;(2)、如图2,过原点O作另一条直线l,交双曲线y= (k>0)于P,Q两点,点P在第一象限.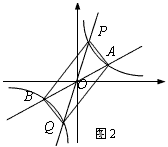
四边形APBQ一定是;
(3)、若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.(4)、设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.26. 如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.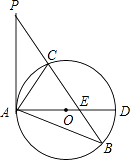 (1)、求证:PA是⊙O的切线;(2)、过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(1)、求证:PA是⊙O的切线;(2)、过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;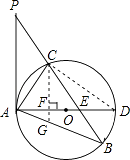 (3)、在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
(3)、在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.