2018年浙江省金华市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-24 类型:中考模拟
一、选择题
-
1. 已知a,b互为相反数,c,d互为倒数,|e|= ,则代数式5(a+b)2+ cd﹣2e的值为( )A、﹣ B、 C、 或﹣ D、﹣ 或2. 一个几何体由若干大小相同的小立方块搭成,图分别是从它的正面、上面看到的形状图,则搭成该几何体的小立方块至少需要( )
 A、5 块 B、6 块 C、7 块 D、8 块3. 以下列各组长度的线段为边,能构成三角形的是( )A、3cm、4cm、8cm B、5cm、5cm、11cm C、12cm、5cm、6cm D、8cm、6cm、4cm4. 如图,△ABC的三个顶点在正方形网格的格点上,则tan∠A的值是( )
A、5 块 B、6 块 C、7 块 D、8 块3. 以下列各组长度的线段为边,能构成三角形的是( )A、3cm、4cm、8cm B、5cm、5cm、11cm C、12cm、5cm、6cm D、8cm、6cm、4cm4. 如图,△ABC的三个顶点在正方形网格的格点上,则tan∠A的值是( )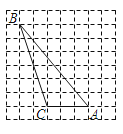 A、 B、 C、 D、5. 下列计算正确的是( )A、a2•a3=a6 B、a6÷a3=a2 C、4x2﹣3x2=1 D、(﹣2a2)3=﹣8a66. 由二次函数y=2(x﹣3)2+1,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=﹣3 C、其最小值为1 D、当x<3时,y随x的增大而增大7. 若小李同学掷出的铅球在场地航砸出一个直径为10厘米,深2厘米的小坑,则该铅球的直径为( )A、20厘米 B、19.5厘米 C、14.5厘米 D、10厘米8. 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1 , 在乙种地板上最终停留在黑色区域的概率为P2 , 则( )
A、 B、 C、 D、5. 下列计算正确的是( )A、a2•a3=a6 B、a6÷a3=a2 C、4x2﹣3x2=1 D、(﹣2a2)3=﹣8a66. 由二次函数y=2(x﹣3)2+1,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=﹣3 C、其最小值为1 D、当x<3时,y随x的增大而增大7. 若小李同学掷出的铅球在场地航砸出一个直径为10厘米,深2厘米的小坑,则该铅球的直径为( )A、20厘米 B、19.5厘米 C、14.5厘米 D、10厘米8. 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1 , 在乙种地板上最终停留在黑色区域的概率为P2 , 则( )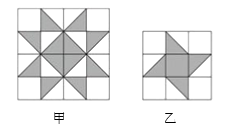 A、 B、 C、 D、以上都有可能9. 若关于 的一元一次不等式组 无解,则 的取值范围是( )A、 ≥1 B、 >1 C、 ≤ D、 <10.
A、 B、 C、 D、以上都有可能9. 若关于 的一元一次不等式组 无解,则 的取值范围是( )A、 ≥1 B、 >1 C、 ≤ D、 <10.如左图,图1表示正六棱柱形状的高式建筑物,图2中的正 六边形部分是从该建筑物的正上方看到的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
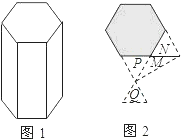 A、P区域 B、Q区域 C、M区域 D、N区域
A、P区域 B、Q区域 C、M区域 D、N区域二、填空题
-
11. 分解因式:x2﹣(x﹣3)2= .12. 已知 则13. 某广告公司全体员工年薪的具体情况如表:
年薪/万元
25
15
10
6
4
人数
1
1
3
3
2
则该公司全体员工年薪的中位数是万元
14. 如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为 .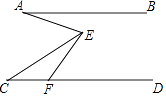 15. 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 .
15. 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 . 16. 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上,C点在斜边上,设矩形的一边AB=xm,矩形的面积为ym2 , 则y的最大值为 .
16. 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上,C点在斜边上,设矩形的一边AB=xm,矩形的面积为ym2 , 则y的最大值为 .
三、解答题
-
17. 计算:( )﹣2﹣( ﹣ )0+2sin30°+|﹣3|.18. 解方程 .19. 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:

①将△ABC向上平移3个单位长度,画出平移后的△A1B1C1 , 写出A1、C1的坐标;②将△A1B1C1绕B1逆时针旋转90°,画出旋转后的△A2B1C2 , 求线段B1C1旋转过程中扫过的面积(结果保留π).
20. 企业举行“爱心一日捐”活动,捐款金额分为五个档次,分别是50元,100元,150元,200元,300元.宣传小组随机抽取部分捐款职工并统计了他们的捐款金额,绘制成两个不完整的统计图,请结合图表中的信息解答下列问题: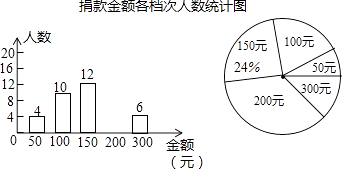 (1)、宣传小组抽取的捐款人数为人,请补全条形统计图;
(1)、宣传小组抽取的捐款人数为人,请补全条形统计图;
(2)、在扇形统计图中,求100元所对应扇形的圆心角的度数;
(3)、已知该企业共有500人参与本次捐款,请你估计捐款总额大约为多少元?
21. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.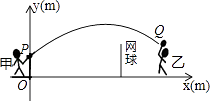 (1)、当a=﹣ 时,
(1)、当a=﹣ 时,①求h的值;
②通过计算判断此球能否过网.
(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.22. 如图,在 Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.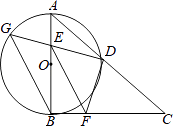 (1)、求证:AE=BF.(2)、连接GB,EF,求证:GB∥EF.(3)、若AE=1,EB=3,求DG的长.23. 如图1,点P为四边形ABCD所在平面上的点,如果∠PAD=∠PBC,则称点P为四边形ABCD关于A、B的等角点,以点C为坐标原点,BC所在直线为x轴建立平面直角坐标系,点B的横坐标为﹣6.
(1)、求证:AE=BF.(2)、连接GB,EF,求证:GB∥EF.(3)、若AE=1,EB=3,求DG的长.23. 如图1,点P为四边形ABCD所在平面上的点,如果∠PAD=∠PBC,则称点P为四边形ABCD关于A、B的等角点,以点C为坐标原点,BC所在直线为x轴建立平面直角坐标系,点B的横坐标为﹣6.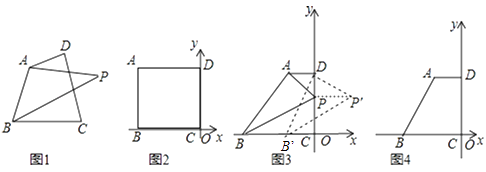 (1)、如图2,若A、D两点的坐标分别为A(﹣6,4)、D(0,4),点P在DC边上,且点P为四边形ABCD关于A、B的等角点,则点P的坐标为;(2)、如图3,若A、D两点的坐标分别为A(﹣2,4)、D(0,4).
(1)、如图2,若A、D两点的坐标分别为A(﹣6,4)、D(0,4),点P在DC边上,且点P为四边形ABCD关于A、B的等角点,则点P的坐标为;(2)、如图3,若A、D两点的坐标分别为A(﹣2,4)、D(0,4).①若P在DC边上时,求四边形ABCD关于A、B的等角点P的坐标;
②在①的条件下,将PB沿x轴向右平移m个单位长度(0<m<6)得到线段P′B′,连接P′D,B′D,试用含m的式子表示P′D2+B′D2 , 并求出使P′D2+B′D2取得最小值时点P′的坐标;
③如图4,若点P为四边形ABCD关于A、B的等角点,且点P坐标为(1,t),求t的值;
④以四边形ABCD的一边为边画四边形,所画的四边形与四边形ABCD有公共部分,若在所画的四边形内存在一点P,使点P分别是各相邻两顶点的等角点,且四对等角都相等,请直接写出所有满足条件的点P的坐标.
24. 如图1所示,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).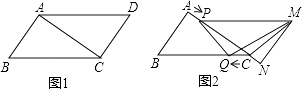 (1)、当t为何值时,PQ∥MN?(2)、设△QMC的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,PQ∥MN?(2)、设△QMC的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.