2018年浙江省嘉兴市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-23 类型:中考模拟
一、选择题
-
1. 计算(﹣9)﹣(﹣3)的结果是( )A、﹣12 B、﹣6 C、+6 D、122. 在下列四个图案中,不是中心对称图形的是( )
A、
B、
B、
C、
C、
D、
D、
3. 2016年12月11日,我国风云四号卫星发射成功,它将停留在距离地面36000公里高的太空,专门用于对固定区域进行气象遥感探测.数据36000用科学记数法表示( )A、3.6×103公里 B、3.6×104公里 C、36×103公里 D、36×104公里4. 某科研小组为了考查某河流野生鱼的数量,从中捕捞200条,作上标记后,放回河里,经过一段时间,再从中捕捞300条,发现有标记的鱼有15条,则估计该河流中有野生鱼( )A、8000条 B、4000条 C、2000条 D、1000条5. 如图,若DC∥FE∥AB,则有( )
3. 2016年12月11日,我国风云四号卫星发射成功,它将停留在距离地面36000公里高的太空,专门用于对固定区域进行气象遥感探测.数据36000用科学记数法表示( )A、3.6×103公里 B、3.6×104公里 C、36×103公里 D、36×104公里4. 某科研小组为了考查某河流野生鱼的数量,从中捕捞200条,作上标记后,放回河里,经过一段时间,再从中捕捞300条,发现有标记的鱼有15条,则估计该河流中有野生鱼( )A、8000条 B、4000条 C、2000条 D、1000条5. 如图,若DC∥FE∥AB,则有( ) A、 B、 C、 D、6. 设的小数部分为b,那么(4+b)b的值是( )A、1 B、是一个有理数 C、3 D、无法确定7. 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
A、 B、 C、 D、6. 设的小数部分为b,那么(4+b)b的值是( )A、1 B、是一个有理数 C、3 D、无法确定7. 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )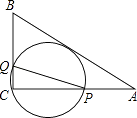 A、5 B、4 C、4.75 D、4.88. 不等式x﹣3≤3x+1的解集在数轴上表示正确的是( )A、
A、5 B、4 C、4.75 D、4.88. 不等式x﹣3≤3x+1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 9.
9.下面是小明按照语句画出的四个图形:(1)直线EF经过点C;(2)点A在直线l外;(3)经过点O的三条线段a、b、c;(4)线段AB、CD相交于点B.他所画图形中,正确的个数是( )
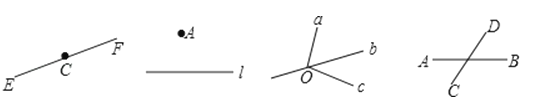 A、1 B、2 C、3 D、410. 如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交 的图象于点Ai , 交直线 于点Bi . 则 的值为( )
A、1 B、2 C、3 D、410. 如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交 的图象于点Ai , 交直线 于点Bi . 则 的值为( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 分解因式:xy2﹣2xy+x= .12. 已知A,B两地相距160km,一辆汽车从A地到B地的速度比原来提高了25%,结果比原来提前0.4h到达,这辆汽车原来的速度是 km/h.13. 现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是14. 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为 .
 15. 一个幻方中,每一行,每一列,及每一对角线上的三个数之和有相同的值,如图所示已知一个幻方中的三个数,x的值是 .
15. 一个幻方中,每一行,每一列,及每一对角线上的三个数之和有相同的值,如图所示已知一个幻方中的三个数,x的值是 .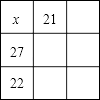 16. 如图,直径为10的⊙A经过点C(0,5)和点0(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为 .
16. 如图,直径为10的⊙A经过点C(0,5)和点0(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为 .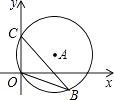
三、解答题
-
17. 计算。(1)、(2)、18. 观察下表:
序号
1
2
3
…
图形
x x
y
x x
x x x
y y
x x x
y y
x x x
x x x x
y y y
x x x x
y y y
x x x x
y y y
x x x x
…
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)、第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;(2)、若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.①求x,y的值;
②在此条件下,第n个特征多项式是否有最小值?若有,求出最小值和相应的n值.若没有,请说明理由.
19. 已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.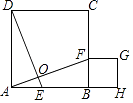 (1)、判断四边形BFGH的形状并证明;(2)、写出图中所有面积相等的图形.20. 如图,一次函数y=x+2的图象与反比例函数y=(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
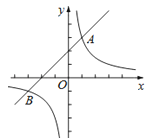
(1)、判断四边形BFGH的形状并证明;(2)、写出图中所有面积相等的图形.20. 如图,一次函数y=x+2的图象与反比例函数y=(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).(1)求反比例函数y=(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
 21. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
21. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: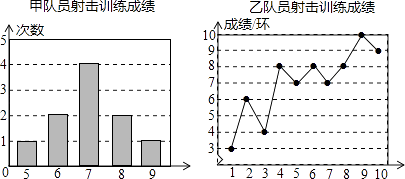
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、写出表格中a,b,c的值;(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?22. 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.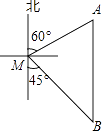 (1)、求渔船从B到A的航行过程中与码头M之间的最小距离.(2)、若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.23. 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)、求渔船从B到A的航行过程中与码头M之间的最小距离.(2)、若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.23. 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.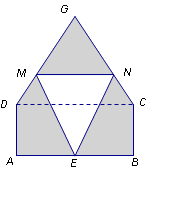 (1)、当MN和AB之间的距离为0.5米时,求此时△EMN的面积;(2)、设MN与AB之间的距离为x 米,试将△EMN的面积S(平方米)表示成关于x的函数;(3)、请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.24. 如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)、当MN和AB之间的距离为0.5米时,求此时△EMN的面积;(2)、设MN与AB之间的距离为x 米,试将△EMN的面积S(平方米)表示成关于x的函数;(3)、请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.24. 如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.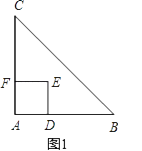 (1)、当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(1)、当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.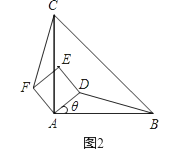 (2)、当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
(2)、当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.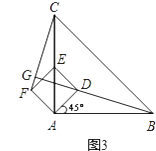
①求证:BD⊥CF;
②当AB=4,AD= 时,求线段BG的长.