内蒙古通辽市库伦旗2017-2018学年九年级上学期数学期末考试试卷
试卷更新日期:2018-05-23 类型:期末考试
一、单选题
-
1. 下列事件是必然事件的是( )A、明天气温会升高 B、随意翻到一本书的某页,这页的页码是奇数 C、早晨太阳会从东方升起 D、某射击运动员射击一次,命中靶心2. 下列四个图形中,既是轴对称图形又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个3. 掷一个骰子时,观察上面的点数,点数为奇数的概率是( ).A、 B、 C、 D、4. 如图,在⊙O中,弦AB,CD相交于点P,若∠A=55°,∠APD=80°,则∠B等于( )
A、4个 B、3个 C、2个 D、1个3. 掷一个骰子时,观察上面的点数,点数为奇数的概率是( ).A、 B、 C、 D、4. 如图,在⊙O中,弦AB,CD相交于点P,若∠A=55°,∠APD=80°,则∠B等于( )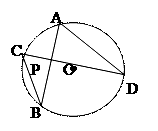 A、40° B、45° C、50° D、55°5. 某城市2014年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2016年底增加到363公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )A、300(1+x)=363 B、300(1+x)2=363 C、300(1+2x)=363 D、363(1-x)2=3006. 若一元二次方程x2+2x+m=0有实数根,则m的取值范围是( )A、m≤-1 B、m≤1 C、m≤4 D、m≤7. 抛物线 的对称轴是( )A、直线x=-2 B、直线 x=2 C、直线x=-3 D、直线x=38. 在平面直角坐标系中,点A(0,-1),点B(4,2),点C在坐标轴上,使∠ACB为直角的点C有( )个A、1 B、2 C、3 D、49. 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( ).
A、40° B、45° C、50° D、55°5. 某城市2014年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2016年底增加到363公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )A、300(1+x)=363 B、300(1+x)2=363 C、300(1+2x)=363 D、363(1-x)2=3006. 若一元二次方程x2+2x+m=0有实数根,则m的取值范围是( )A、m≤-1 B、m≤1 C、m≤4 D、m≤7. 抛物线 的对称轴是( )A、直线x=-2 B、直线 x=2 C、直线x=-3 D、直线x=38. 在平面直角坐标系中,点A(0,-1),点B(4,2),点C在坐标轴上,使∠ACB为直角的点C有( )个A、1 B、2 C、3 D、49. 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( ).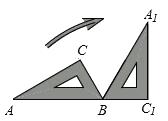
A、120° B、90° C、60° D、30°10. 已知 的图像如图所示,则 的方程的两实根 ,则满足( )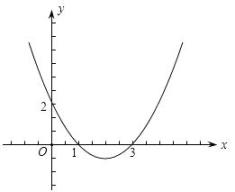 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知x=1是一元二次方程 的一个根,则 的值为.12. 如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1、2、3、4、5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为 (偶数),指针指向标有奇数所在区域的概率为 (奇数),则 (偶数) (奇数)(填“ ”“ ”或“ ”).
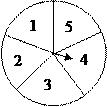 13. 有一个亭子的地基如图所示,它是一个半径为4 m的正六边形,它的面积是(保留根号).
13. 有一个亭子的地基如图所示,它是一个半径为4 m的正六边形,它的面积是(保留根号).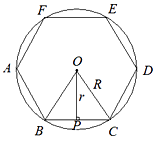 14. 如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2 .则阴影部分的面积为.
14. 如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2 .则阴影部分的面积为.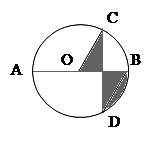 15. 在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米 ,则修建的路宽应为.
15. 在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米 ,则修建的路宽应为.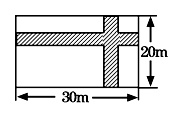 16. 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是 元(结果保留整数).
16. 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是 元(结果保留整数).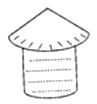 17. 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
17. 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .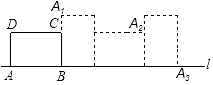
三、解答题
-
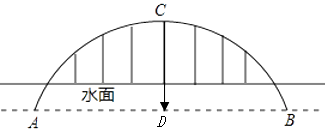
18. 巫山长江公路大桥是一个中承式钢管砼圆弧形拱桥,主跨度AB=492米,拱桥最高点C距水面100米,求该拱桥的半径是多少米?
 19. 小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如下图:
19. 小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如下图: (1)、请你完成下面表示游戏一个回合所有可能出现的结果的树状图;(2)、求一个回合能确定两人先下棋的概率.20. 如图,在⊙O中,
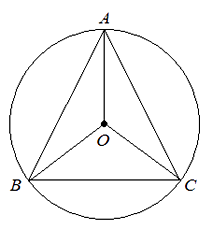
(1)、请你完成下面表示游戏一个回合所有可能出现的结果的树状图;(2)、求一个回合能确定两人先下棋的概率.20. 如图,在⊙O中,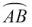 =
=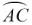 ,∠ACB=60°,
,∠ACB=60°,求证∠AOB=∠BOC=∠COA.
 21. 如图,在 中, , ,将 绕点 沿逆时针方向旋转 得到 .
21. 如图,在 中, , ,将 绕点 沿逆时针方向旋转 得到 .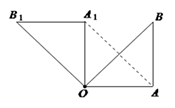 (1)、线段 的长是 , 的度数是;(2)、连结 ,求证:四边形 是平行四边形;(3)、求四边形 的面积.22. 王老汉为了与顾客签订购销合同,对自己鱼塘中鱼的总质量进行了估计,第一次捞出100条,称得质量为184千克.并将每条鱼做上记号后放入水中,当它们完全混合于鱼群后,又捞出200条,称得质量为416千克,且带有记号的鱼有20条,王老汉的鱼塘中估计有鱼多少条鱼?总质量为多少千克?23. 已知二次函数y=a -4x+c的图像经过点A和点B.
(1)、线段 的长是 , 的度数是;(2)、连结 ,求证:四边形 是平行四边形;(3)、求四边形 的面积.22. 王老汉为了与顾客签订购销合同,对自己鱼塘中鱼的总质量进行了估计,第一次捞出100条,称得质量为184千克.并将每条鱼做上记号后放入水中,当它们完全混合于鱼群后,又捞出200条,称得质量为416千克,且带有记号的鱼有20条,王老汉的鱼塘中估计有鱼多少条鱼?总质量为多少千克?23. 已知二次函数y=a -4x+c的图像经过点A和点B.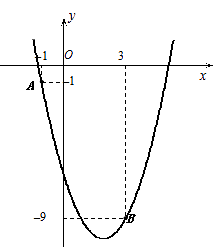 (1)、求该二次函数的表达式;(2)、写出该抛物线的对称轴及顶点坐标;(3)、点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离24. 如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
(1)、求该二次函数的表达式;(2)、写出该抛物线的对称轴及顶点坐标;(3)、点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离24. 如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,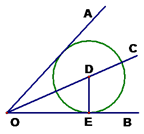
①判断⊙D与OA的位置关系,并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
25. 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).(1)、当每吨售价是240元时,计算此时的月销售量;(2)、求出y与x的函数关系式(不要求写出x的取值范围);(3)、该经销店要获得最大月利润,售价应定为每吨多少元?26. 如图,⊙O的直径AB=2,AM、BN是它的两条切线,CD与⊙O相切于点E,与BN、AM交于点C、D,设AD=x,BC=y。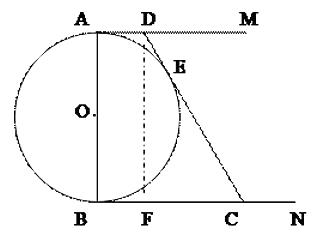 (1)、求证:AM∥BN。(2)、求y关于x的函数关系式。(3)、若x、y是关于t的方程2t -5t+m=0的两根,且xy= ,求x、y的值。
(1)、求证:AM∥BN。(2)、求y关于x的函数关系式。(3)、若x、y是关于t的方程2t -5t+m=0的两根,且xy= ,求x、y的值。