内蒙古呼伦贝尔市根河一中2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2018-05-23 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 式子 1x−2 在实数范围内有意义，则x的取值范围（   ）
    A、x≤2 B、x＞2 C、x＜2 D、x≥2

    查看试题解析

  • 2. 将函数y=-3x的图象沿y轴向上平移2个单位长度后，所得图象对应的函数关系式为（  ）
    A、y=-3x+2 B、y=-3x-2 C、y=-3（x+2） D、y=-3（x-2）

    查看试题解析

  • 3. 某校组织数学学科竞赛为参加区级比赛做选手选拔工作，经过多次测试后，有四位同学成为晋级的候选人，具体情况如下表，如果从这四位同学中选出一名晋级（总体水平高且状态稳定）你会推荐（   ）


    甲

    乙

    丙

    丁

    平均分

    92

    94

    94

    92

    方 差

    35

    35

    23

    23

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 4. 下列各命题的逆命题成立的是（  ）
    A、全等三角形的对应角相等 B、如果两个数相等，那么它们的绝对值相等 C、两直线平行，同位角相等 D、如果两个角都是45°，那么这两个角相等

    查看试题解析

  • 5. 若一次函数y=ax+b的图象经过第一、二、四象限，则下列不等式中总是成立的是（   ）
    A、ab＞0 B、a-b＞0 C、a2+b＞0 D、a+b＞0

    查看试题解析

  • 6. 矩形、菱形、正方形都具有的性质是（　　）

    A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分对角

    查看试题解析

  • 7. 如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（   ）

    A、x＜ 32 B、x＜3 C、x＞ 32 D、x＞3

    查看试题解析

  • 8. 小丽从家出发开车前去观看球赛，途中发现忘了带门票，于是打电话让妈妈马上从家里送来，同时小丽也往回开，遇到妈妈后聊了一会儿，接着继续开车前往比赛场．设小丽从家出发后所用时间为t，小丽与比赛现场的距离为S．如图能反映S与t的函数关系的大致图象是（    ）
    A、 B、   C、 D、

    查看试题解析

  • 9. 如图，一次函数y=（m-1）x+m-3的图象分别于x轴、y轴的负半轴相交于点A、B，则m的取值范围是（   ）

    A、m＞3 B、m＜3 C、m＞1 D、m＜1

    查看试题解析

  • 10. 如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为（   ）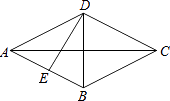

    A、2.4cm B、4.8cm C、5cm D、9.6cm

    查看试题解析

二、填空题

  • 11. 已知一组数据3，2，5，4，1，则这组数据的方差是.

    查看试题解析

  • 12. 如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边  于点E，且AE=3，则AB的长为.

    查看试题解析

  • 13. 已知函数y=(k-1)x|k|是正比例函数，则k=

    查看试题解析

  • 14. 一次函数y= -3x+9的图象与x轴交点坐标是

    查看试题解析

  • 15. 已知一次函数y=kx+b的图象与直线y=-x+1平行，且过点（1，-2），那么此一次函数的解析式为 ．

    查看试题解析

  • 16. 已知关于x的方程mx+3=4的解为x=1，则直线y=（m-2）x-3一定不经过第象限．

    查看试题解析

  • 17. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=6，BC=8，则EF的长为 ．

    查看试题解析

  • 18. 如图，把一张矩形的纸沿对角线BD折叠，若AD=8，AB=6，则BE= ．

    查看试题解析

三、解答题

  • 19. 512-913+1248

    查看试题解析

  • 20. (7+5)(7−5)+(27−12)÷3

    查看试题解析

  • 21. 已知：y与x+2成正比例，且x=1时，y=-6．
    (1)、求y与x之间的函数关系式
    (2)、若点M（m，2）在这个函数的图象上，求m的值．

    查看试题解析

  • 22. 如图，平行四边形ABCD中，∠ABC=60°，点E，F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，CF= 23 。
    (1)、求证：四边形ABDE是平行四边形；
    (2)、求AB的长。

    查看试题解析

  • 23. 如图，在矩形ABCD中，∠BAD的平分线交BC于点E，O为对角线AC、BD的交点，且∠CAE=15° .

    (1)、求证：△AOB为等边三角形；
    (2)、求∠BOE度数．

    查看试题解析

  • 24. 某校八年级全体同学参加了某项捐款活动，随机抽查了部分同学捐款的情况统计如图所示．

    (1)、本次共抽查学生人，并将条形图补充完整；
    (2)、捐款金额的众数是平均数是中位数为
    (3)、在八年级600名学生中，捐款20元及以上（含20元）的学生估计有多少人？

    查看试题解析

  • 25. 直线y=2x+m（m＞0）与x轴交于点A（-2，0），直线y=-x+n（n＞0）与x轴、y轴分别交于B、C两点，并与直线y=2x+m（m＞0）相交于点D，若AB=4．

    (1)、求点D的坐标；
    (2)、求出四边形AOCD的面积；
    (3)、若点P为x轴上一动点，且使PD+PC的值最小，不写过程，直接写出点P的坐标。

    查看试题解析

  • 26. 在茶节期间，某茶商订购了甲种茶叶90吨，乙种茶叶80吨，准备用A、B两种型号的货车共20辆运往外地．已知A型货车每辆运费为0.4万元，B型货车每辆运费为0.6万元。
    (1)、设A型货车安排x辆，总运费为y万元，写出y与x的函数关系式；
    (2)、若一辆A型货车可装甲种茶叶6吨，乙种茶叶2吨；一辆B型货车可装甲种茶叶3吨，乙种茶叶7吨．按此要求安排A、B两种型号货车一次性运完这批茶叶，共有哪几种运输方案？
    (3)、说明哪种方案运费最少？最少运费是多少万元？

    查看试题解析