内蒙古包头市青山区2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-05-23 类型:期末考试
一、单选题
-
1. 在下列四组数中,不是勾股数的一组数是( )A、a=15,b=8,c=17 B、a=9,b=12,c=15 C、a=7,b=24,c=25 D、a=3,b=5,c=72. 下列计算正确的是( )A、 =±3 B、 =-2 C、 =-3 D、3. 一组数据5,2,6,9,5,3的众数、中位数、平均数分别是( )A、5,5,6 B、9,5,5 C、5,5,5 D、2,6,54. 点P(1,-2)关于y轴对称的点的坐标是( )A、(1,2) B、(-1,2) C、(-1,-2) D、(-2,1)5. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
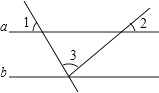 A、40° B、60° C、80° D、100°6. 如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解( )
A、40° B、60° C、80° D、100°6. 如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解( )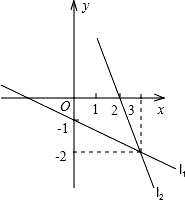 A、 B、 C、 D、7. 若kb>0,则函数y=kx+b的图象可能是( )A、
A、 B、 C、 D、7. 若kb>0,则函数y=kx+b的图象可能是( )A、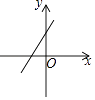 B、
B、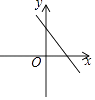 C、
C、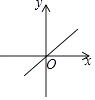 D、
D、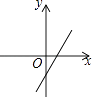 8. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=39. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )
8. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=39. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )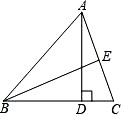 A、15° B、20° C、25° D、30°10. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A、15° B、20° C、25° D、30°10. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )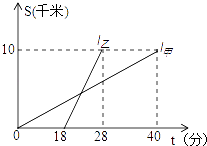 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为S甲2=16.7,乙比赛成绩的方差为S乙2=28.3,那么成绩比较稳定的是(填“甲”或“乙”)12. 已知一个正数的平方根是3x-2和5x-6,则这个数是 .13. 要把一张面值10元的人民币换成零钱,现有足够的面值为2元,1元的人民币,那么共有种换法。14. 如果将一副三角板按如图方式叠放,那么∠1= .
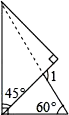 15. 已知 ,则 = .16. 小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为米.17. 一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了道题.18. 如图,长方形ABCD中,AB=5,AD=3,点P从点A出发,沿长方形ABCD的边逆时针运动,设点P运动的距离为x;△APC的面积为y,如果5<x<8,那么y关于x的函数关系式为 .
15. 已知 ,则 = .16. 小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为米.17. 一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了道题.18. 如图,长方形ABCD中,AB=5,AD=3,点P从点A出发,沿长方形ABCD的边逆时针运动,设点P运动的距离为x;△APC的面积为y,如果5<x<8,那么y关于x的函数关系式为 .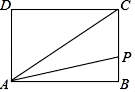
三、解答题
-
19. 计算:(1)、 ,(2)、20. 解方程组:(1)、 ;(2)、 .21. A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
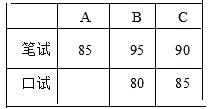
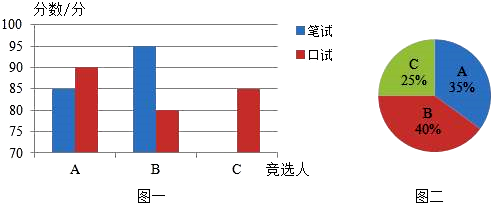 (1)、请将表一和图一中的空缺部分补充完整.(2)、竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.(3)、若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.22. 列方程组解应用题:
(1)、请将表一和图一中的空缺部分补充完整.(2)、竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.(3)、若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.22. 列方程组解应用题:为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A
B
价格(万元/台)
a
b
节省的油量(万升/年)
2.4
2
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)、请求出a和b;(2)、若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?23. 如图,已知直线AB∥CD,∠A=∠C=100°,E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.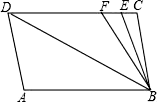 (1)、求证:AD∥BC;(2)、求∠DBE的度数;(3)、若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由.24. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)、求证:AD∥BC;(2)、求∠DBE的度数;(3)、若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由.24. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.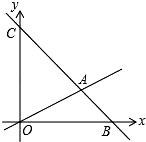 (1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在求出此时点M的坐标;若不存在,说明理由.
(1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在求出此时点M的坐标;若不存在,说明理由.