山西阳泉盂县2016-2017学年九年级上学期数学期末考试试卷
试卷更新日期：2018-05-23 类型：期末考试
一、单选题
-
1. 点M（1，-2）关于原点对称的点的坐标是（ ）A、（-1，2） B、（1，2） C、（-1，-2） D、（-2，1）2. 若反比例函数y= （k≠0）的图象经过点P（-2，3），则该函数的图象不经过的点是（ ）A、（3，-2） B、（1，-6） C、（-1，6） D、（-1，-6）3.
如图的两个四边形相似，则∠α的度数是（ ）
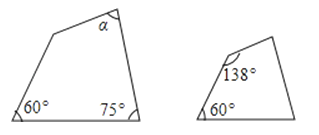A、87° B、60° C、75° D、120°4. 已知关于x的一元二次方程x2+ax+b=0有一个非零根-b，则a-b的值为（ ）A、-1 B、0 C、1 D、-25. 如果一个扇形的半径是1，弧长是 ，那么此扇形的圆心角的大小为（ ）A、30° B、45° C、60° D、90°6. 在Rt△ABC中，∠C=90°，∠B=35°，AB=7，则BC的长为（ ）A、7sin35° B、7cos35° C、7tan35° D、7. 对于反比例函数y= ，当x≤-6时，y的取值范围是（ ）A、y≥-1 B、y≤-1 C、-1≤y＜0 D、y≥18. 如图是以△ABC的边AB为直径的半圆O，点C恰好在半圆上，过C作CD⊥AB交AB于D．已知cos∠ACD= ，BC=4，则AC的长为（ ）
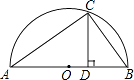A、1 B、 C、3 D、9.在研究相似问题时，甲、乙同学的观点如下：
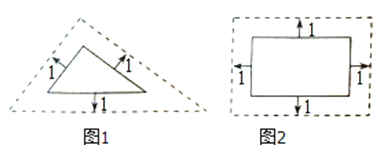
甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．
乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形相似．
对于两人的观点，下列说法正确的是（ ）
A、甲对，乙不对 B、甲不对，乙对 C、两人都对 D、两人都不对10. 二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：x
…
-3
-2
-1
0
1
…
y
…
-6
0
4
6
6
…
给出下列说法：
①抛物线与y轴的交点为（0，6）；②抛物线的对称轴在y轴的左侧；③抛物线一定经过（3，0）点；④在对称轴左侧y随x的增大而减增大．从表中可知，其中正确的个数为（ ）
A、4 B、3 C、2 D、1二、填空题
-
11. 已知四条线段满足a= ，将它改写成为比例式为（写出你认为正确的一个）．12. 若点P（2，6）、点Q（-3，b）都是反比例函数y= （k≠0）图象上的点，则b= ．13. 如图，在⊙O中，已知半径为5，弦AB的长为8，那么圆心O到AB的距离为 ．
14. 已知抛物线y=ax2+bx+c（a≠0）与x轴交于A，B两点，若点A的坐标为（-2，0），抛物线的对称轴为直线x=2，则线段AB的长为 ．15. 如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AC= ，∠B=60°，则CD的长为 ．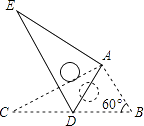
16. 下列事件：①随意翻到一本书的某页，这页的页码是奇数；
②测得某天的最高气温是100℃；
③掷一次骰子，向上一面的数字是2；
④度量四边形的内角和，结果是360°．
其中是随机事件的是 ． （填序号）
三、解答题
-
17.
(1)、解方程3x（x-2）=2（2-x）．(2)、计算：2cos60°-3tan30°+2tan45°．18. 如图，△ABC在方格纸中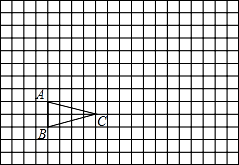
(1)、请在方格纸上建立平面直角坐标系，使A（2，3），C（6，2），并求出B点坐标；
(2)、以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形△A′B′C′；(3)、计算△A′B′C′的面积S．19. 如图所示，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．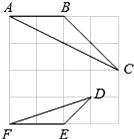
(1)、填空：∠ABC= ， BC=；(2)、判断△ABC与△DEF是否相似？并证明你的结论．20. 某超市计划在“十周年”庆典当天开展购物抽奖活动，凡当天在该超市购物的顾客，均有一次抽奖的机会，抽奖规则如下：将如图所示的圆形转盘平均分成四个扇形，分别标上1，2，3，4四个数字，抽奖者连续转动转盘两次，当每次转盘停止后指针所指扇形内的数为每次所得的数（若指针指在分界线时重转）；当两次所得数字之和为8时，返现金20元；当两次所得数字之和为7时，返现金15元；当两次所得数字之和为6时返现金10元．
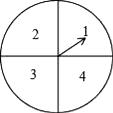(1)、试用树状图或列表的方法表示出一次抽奖所有可能出现的结果；(2)、某顾客参加一次抽奖，能获得返还现金的概率是多少？21. 如图，一游客在某城市旅游期间，沿街步行前往著名的电视塔观光，他在A处望塔顶C的仰角为30°，继续前行250m后到达B处，此时望塔顶的仰角为45°．已知这位游客的眼睛到地面的距离约为170cm，假若游客所走路线直达电视塔底．请你计算这座电视塔大约有多高？（结果保留整数. ≈1.7， ≈1.4；E，F分别是两次测量时游客眼睛所在的位置．）
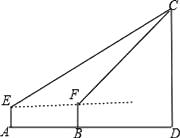22. 已知反比例函数y= （m为常数）的图象在一、三象限．
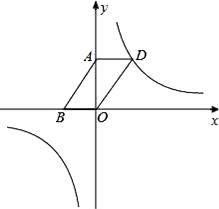(1)、求m的取值范围；(2)、如图，若该反比例函数的图象经过▱ABOD的顶点D，点A、B的坐标分别为（0，3），（-2，0）．①求出函数解析式；
②设点P是该反比例函数图象上的一点，若OD=OP，则P点的坐标为 ▲ ；若以D、O、P为顶点的三角形是等腰三角形，则满足条件的点P的个数为 ▲ 个．
23. 如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．
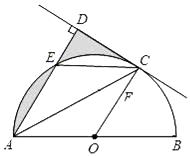(1)、判断CD与⊙O的位置关系，并证明你的结论；(2)、若E是弧AC的中点，⊙O的半径为1，求图中阴影部分的面积．24. 如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．
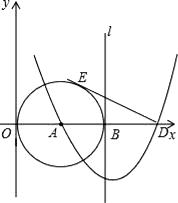(1)、以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；(2)、抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求此切线长；(3)、点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长．