2018年浙江省湖州市中考数学冲刺模拟卷（3）

试卷更新日期：2018-05-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 3的相反数是（）

A、﹣3 B、﹣ $\frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. 已知代数式x+2y的值是3，则代数式2x+4y+1的值是（　　）

A、1 B、4 C、7 D、不能确定

查看试题解析
3. 16的算术平方根是（）

A、16 B、4 C、﹣4 D、±4

查看试题解析
4.
如图，等边三角形ABC内接于⊙O，若边长为4 $\sqrt{3}$ cm，则⊙O的半径为（　　）

A、6cm B、4cm C、2cm D、2 $\sqrt{3}$ cm

查看试题解析
5. 下面说法：
①如果一组数据的众数是5，那么这组数据中出现次数最多的数是5；
②如果一组数据的平均数是0，那么这组数据的中位数为0；
③如果一组数据1，2，x，4的中位数是3，那么x=4；
④如果一组数据的平均数是正数，那么这组数据都是正数．
其中错误的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（）

A、10 B、7 C、5 D、4

查看试题解析
7. 若我们把十位上的数字比个位和百位上的数字都大的三位数称为凸数，如：786，465．则由1，2，3这三个数字构成的，数字不重复的三位数是“凸数”的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、

查看试题解析
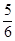8. 如图，AB与⊙O相切于点A，BO与⊙O相交于点C，点D是优弧AC上一点，∠CDA=27°，则∠B的大小是（）

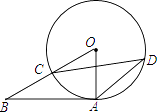A、27° B、34° C、36° D、54°

查看试题解析
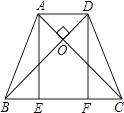
9.
如图，在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD于O，AE⊥BC，DF⊥BC，垂足分别为E、F，AD=4，BC=8，则AE+EF等于(　　)

A、9　 B、10 C、11 D、12

查看试题解析
10. 如图，A，B两点在反比例函数y= $\frac{k_{1}}{x}$ 的图象上，C，D两点在反比例函数y= $\frac{k_{2}}{x}$ 的图象上，AC⊥y轴于点E，BD⊥y轴于点F，AC=2，BD=1，EF=3，则k₁﹣k₂的值是（）

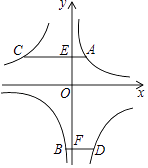A、6 B、4 C、3 D、2

查看试题解析

二、填空题

11. 计算：|﹣3|+（﹣1）²= ．

查看试题解析
12. 在函数y= $\frac{x}{x - 6}$ 中，自变量x的取值范围是．

查看试题解析
13. 一家公司打算招聘一名英文翻译，对甲、乙两名应试者进行了听、说、读、写的英语水平测试，他们的各项成绩（百分制）如下：
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3：3：2：2的比确定，应该录取（填“甲”或“乙”）

查看试题解析
14.
如图，在矩形ABCD中，AB=4，AD=2，以点A为圆心，AB长为半径画圆弧交边DC于点E，则的长度为 .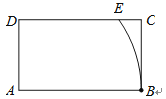

查看试题解析
15.
已知抛物线y=ax²﹣4ax+c经过点A（0，2），顶点B的纵坐标为3．将直线AB向下平移，与x轴、y轴分别交于点C、D，与抛物线的一个交点为P，若D是线段CP的中点，则点P的坐标为．

查看试题解析
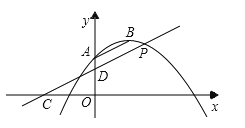16.
如图，有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ，连接EF、GH得到四边形EFGH，设S_{四边形ABCD}=S₁ ， S_{四边形EFGH}=S₂ ， S_{四边形MNPQ}=S₃ ，若S₁+S₂+S₃=10，则S₂= ．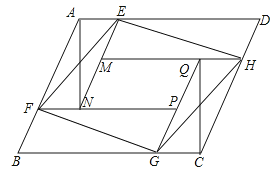

查看试题解析

三、解答题

17. 先化简：（ $\frac{x + 1}{x - 1}$ +1）÷ $\frac{x^{2} + x}{x^{2} - 2 x + 1}$ + $\frac{2 - 2 x}{x^{2} - 1}$ ，然后从﹣2≤x≤2的范围内选取一个合适的整数作为x的值代入求值．

查看试题解析
18. 解不等式组 ${\begin{matrix} 5 x + 1 > 3 (x - 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{matrix}$ ，并把它的解集在数轴上表示出来．

查看试题解析
19. 在平面直角坐标系xOy中，已知一次函数的图象经过点（2，3）与（﹣3，﹣7）．

(1)、求这个一次函数的解析式；

(2)、求这个一次函数的图象与x轴、y轴的交点坐标．

查看试题解析
20.
如图，AB是⊙O的直径，C是的中点，CE⊥AB于E，BD交CE于点F，

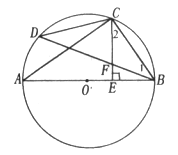
（1）求证：CF＝BF；
（2）若CD＝12，AC＝16，求⊙O的半径和CE的长。

查看试题解析
21. 今年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点．为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的三种统计图表．
对雾霾了解程度的统计表：
对雾霾的了解程度
百分比
A．非常了解
5%
B．比较了解
m
C．基本了解
45%
D．不了解
n
请结合统计图表，回答下列问题．
对雾霾天气了解程度的条形统计图
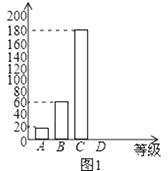
对雾霾天气了解程度的扇形统计图

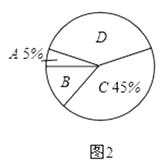(1)、本次参与调查的学生共有人，m= ， n=；

(2)、图2所示的扇形统计图中D部分扇形所对应的圆心角是度；

(3)、请补全图1示数的条形统计图；

(4)、根据调查结果，学校准备开展关于雾霾知识竞赛，某班要从“非常了解”态度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．

查看试题解析
22. 今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．

(1)、试问去年每吨大蒜的平均价格是多少元？

(2)、该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？

查看试题解析
23.
如图①，△ABC的角平分线BD、CE相交于点P.
（1）如果∠A=70°，求∠BPC的度数；
（2）如图②，过P点作直线MN∥BC，分别交AB和AC于点M和N，试求∠MPB+∠NPC的度数（用含∠A的代数式表示）；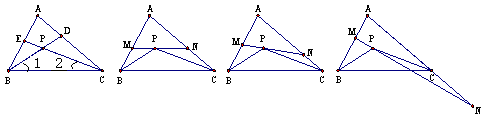

① ② ③ ④
在（2）的条件下，将直线MN绕点P旋转.
（ⅰ）当直线MN与AB、AC的交点仍分别在线段AB和AC上时，如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由；
（ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（ⅰ）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若成立，请说明你的理由；若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由.

查看试题解析
24.
如图，已知抛物线y=ax²+bx+c（a≠0）的顶点坐标为Q（2，﹣1），且与y轴交于点C（0，3），与x轴交于A，B两点（点A在点B的右侧），点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．

(1)、求该抛物线的函数关系式；

(2)、当△ADP是直角三角形时，求点P的坐标；

(3)、在题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

查看试题解析

对雾霾的了解程度	百分比
A．非常了解	5%
B．比较了解	m
C．基本了解	45%
D．不了解	n

应试者	听	说	读	写
甲	85	83	78	75
乙	73	80	85	82