山西省运城市垣曲县2017-2018学年九年级上学期数学期末考试试卷
试卷更新日期：2018-05-23 类型：期末考试
一、单选题
-
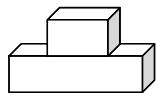
1. 一元二次方程x2-3x=0的解是（ ）A、x1=0，x2=-3 B、x=-3 C、x=3 D、x1=0，x2=32. cos60°的值为（ ）A、 B、 C、 D、3. 如图，从左面观察这个立体图形，能得到的平面图形是（ ）
A、
B、
C、
D、
4. 如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上.若AB=6，BC=9，则BF的长为（ ）
A、4 B、3 C、4.5 D、55. 我们学习了一次函数、二次函数和反比例函数，回顾学习过程，都是按照列表、描点、连线得到函数的图象，然后根据函数的图象研究函数的性质，这种研究方法主要体现的数学思想是（ ）A、演绎 B、数形结合 C、抽象 D、公理化6. 要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场，根据时间和场地等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ）A、 x(x+1)=28 B、 x(x-1)=28 C、x(x+1)=28 D、x(x-1)=287. 在同一直角坐标系中，函数y=2x+3与y= 的图象可能是（ ）A、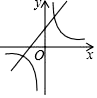
B、
C、
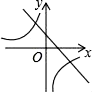D、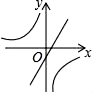
8. 如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1： ，点A的坐标为（1，0），则E点的坐标为（ ）
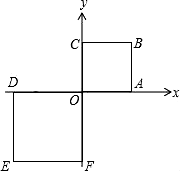A、（- ，0） B、（- ，- ） C、（- ，- ） D、（-2，-2）9. 抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如下图，则以下结论：①b2-4ac＜0；②a+b+c＜0；③c-a=2；④方程ax2+bx+c-2=0有两个相等的实数根.其中正确结论的个数为（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
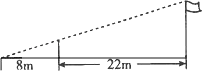
10. 关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根，则k的取值范围是.11. 如图，为测量学校旗杆的高度，小东用长为3.2m的竹竿做测量工具．移动竹竿使竹竿，旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为 m．
12. 如图，菱形OABC的顶点O是原点，顶点B在y轴上，菱形的两条对角线的长分别是6和4，反比例函数y= （x＜0）的图象经过点C，则k的值为.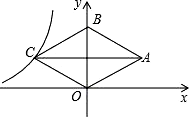
13. 如图，在2×2的正方形网格中有9个格点，已知取定点A和B，在余下的7个点中任取一点C，使△ABC为直角三角形的概率是.
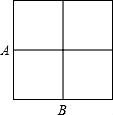14. 如图，已知点C为线段AB的中点，CD⊥AB且CD=AB=4，连接AD，BE⊥AB，AE是 的平分线，与DC相交于点F，EH⊥DC于点G，交AD于点H，则HG的长为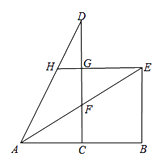
三、解答题
-
15. 请分别计算：
(1)、（- ）-1×（-1-2）-（π-2018）0+|-2|tan45°(2)、x2-6x+5=016. 在一个不透明的布袋里装有4个标有1，2，3，4的小球，它们的形状、大小完全相同，小明从布袋里随机取出一个小球，记下数字为x，小红在剩下的3个小球中随机取出一个小球，记下数字为y(1)、计算由x、y确定的点（x，y）在函数y=-x+5的图象上的概率.(2)、小明和小红约定做一个游戏，其规则为：若x、y满足xy＞6，则小明胜；若x、y满足xy＜6，则小红胜，这个游戏公平吗？请说明理由；若不公平，请写出公平的游戏规则.17. 如图，点D在△ABC的AB边上，且∠ACD=∠A.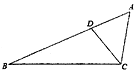
(1)、作∠BDC的平分线DE，交BC于点F（用尺规作图法，保留作图痕迹，不要求写作法）；(2)、在(1)的条件下，判断直线DE与直线AC的位置关系，并说明理由.18. 如图，反比例函数y= 的图象与一次函数y=kx+b的图象交于点A，B，点A、B的横坐标分别为1，-2，一次函数图象与y轴的交于点C，与x轴交于点D.
(1)、求一次函数的解析式；(2)、对于反比例函数y= ，当y＜-1时，写出x的取值范围；(3)、在第三象限的反比例图象上是否存在一个点P，使得S△ODP=2S△OCA？若存在，请求出点P的坐标；若不存在，请说明理由.19. 如图，小明坐在堤边A处垂钓，河堤AC与水平面的夹角为30°，AC的长为 米，钓竿AO与水平线的夹角为60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离.
20. 某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元.每提高一个档次，每件利润增加2元，但一天产量减少5件.(1)、若生产第x档次的产品一天的总利润为y元（x为正整数，且1≤x≤10），求y关于x的函数关系式；(2)、若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次.21. 阅读理解：如图①，在四边形ABCD的边AB上任取一点E（点E不与A、B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的“相似点”；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的“强相似点”．解决问题：
(1)、如图①，∠A=∠B=∠DEC=45°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；(2)、如图②，在矩形ABCD中，A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图②中画出矩形ABCD的边AB上的强相似点；(3)、如图③，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB与BC的数量关系．22. 综合探究：如图1，在平面直角坐标系xOy中，抛物线y=- +bx+8与x轴交于点A（-6，0）和点B（点A在点B左侧），与y轴交于点C，点P为线段AO上的一个动点，过点P作x轴的垂线l与抛物线交于点E，连接AE、EC.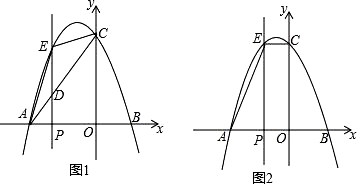
(1)、求抛物线的表达式及点C的坐标；(2)、连接AC交直线l于点D，则在点P运动过程中，当点D为EP中点时，S△ADP：S△CDE=；(3)、如图2，当EC∥x轴时，点P停止运动，此时，在抛物线上是否存在点G，使得以点A、E、G为顶点的三角形是直角三角形？若存在，请求出点G的坐标，若不存在，说明理由.