山西省晋中市灵石县2017-2018学年九年级上学期数学期末考试试卷
试卷更新日期:2018-05-23 类型:期末考试
一、单选题
-
1. 如果一元二次方程2x2+3x+m=0有两个相等的实数根,那么实数m的取值为( )A、m> B、m C、m= D、m=2. 如图所示,该几何体的左视图是( )
 A、
A、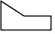 B、
B、 C、
C、 D、
D、 3. 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡的坡度为( )
3. 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡的坡度为( )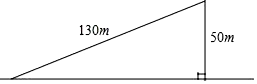 A、 B、 C、 D、4. 函数y1=ax2+b,y2= (ab<0)的图象在下列四个示意图中,可能正确的是( )A、
A、 B、 C、 D、4. 函数y1=ax2+b,y2= (ab<0)的图象在下列四个示意图中,可能正确的是( )A、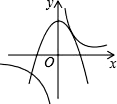 B、
B、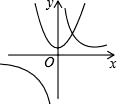 C、
C、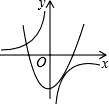 D、
D、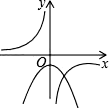 5. 二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
5. 二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x
…
-3
-2
-1
0
1
…
y
…
-3
-2
-3
-6
-11
…
则该函数图象的顶点坐标为( )
A、(-3,-3) B、(-2,-2) C、(-1,-3) D、(0,-6)6. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )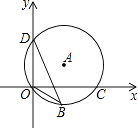 A、 B、 C、 D、7. 若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为( )A、18° B、36° C、72° D、144°8. 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
A、 B、 C、 D、7. 若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为( )A、18° B、36° C、72° D、144°8. 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )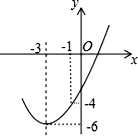 A、b2>4ac B、ax2+bx+c≥-6 C、若点(-2,m),(-5,n)在抛物线上,则m>n D、关于x的一元二次方程ax2+bx+c=-4的两根为-5和-19. 将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价( )A、5元 B、10元 C、15元 D、20元10. 如图,将函数y= (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A、b2>4ac B、ax2+bx+c≥-6 C、若点(-2,m),(-5,n)在抛物线上,则m>n D、关于x的一元二次方程ax2+bx+c=-4的两根为-5和-19. 将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价( )A、5元 B、10元 C、15元 D、20元10. 如图,将函数y= (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )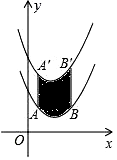 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, ,则 = .
 12. 双曲线y1、y2在第一象限的图象如图, ,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 .
12. 双曲线y1、y2在第一象限的图象如图, ,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 .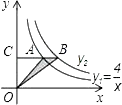 13. 如图,四边形ABCD内接于⊙O,∠DAB=120°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为度(写出一个即可).
13. 如图,四边形ABCD内接于⊙O,∠DAB=120°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为度(写出一个即可).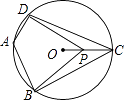 14. 如图,平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=6,AF=4,cos∠EAF= ,则CF= .
14. 如图,平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=6,AF=4,cos∠EAF= ,则CF= .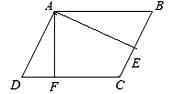 15. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.
15. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.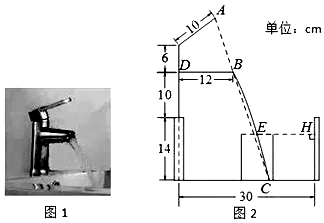
三、解答题
-
16. 按要求完成下列各题:(1)、解方程x2-6x-4=0(用配方法)(2)、计算:tan260°-2cos60°- sin45°17. 为了传承祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
九宫格
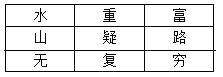 (1)、小明回答该问题时,仅对第二个字是选“重”还是选“穷”难以抉择,随机选择其中一个,则小明回答正确的概率是;(2)、小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.
(1)、小明回答该问题时,仅对第二个字是选“重”还是选“穷”难以抉择,随机选择其中一个,则小明回答正确的概率是;(2)、小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.
18. 如图,已知A(-4,2),B(n,-4)两点是一次函数y=kx+b和反比例函数y= 的图象的两个交点.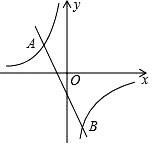 (1)、求反比例函数的表达式和n的值;(2)、观察图象,直接写出不等式kx+b- >0的解集.19. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)、求反比例函数的表达式和n的值;(2)、观察图象,直接写出不等式kx+b- >0的解集.19. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.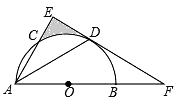 (1)、求证:EF为半圆O的切线;(2)、若DA=DF= ,求阴影区域的面积.(结果保留根号和π)20. 汾河孕育着世代的龙城子孙,而魅力汾河两岸那“新外滩”的称号,将太原人对汾河的爱表露无遗…贯穿太原的汾河,让桥,也成为太原的文化符号,让汾河两岸,也成为繁华的必争之地!北中环桥是世界上首座对称五拱反对称五跨非对称斜拉索桥,2013年开工建设,当年实现全线竣工通车.这座桥造型现代,宛如一条腾飞巨龙.
(1)、求证:EF为半圆O的切线;(2)、若DA=DF= ,求阴影区域的面积.(结果保留根号和π)20. 汾河孕育着世代的龙城子孙,而魅力汾河两岸那“新外滩”的称号,将太原人对汾河的爱表露无遗…贯穿太原的汾河,让桥,也成为太原的文化符号,让汾河两岸,也成为繁华的必争之地!北中环桥是世界上首座对称五拱反对称五跨非对称斜拉索桥,2013年开工建设,当年实现全线竣工通车.这座桥造型现代,宛如一条腾飞巨龙.小芸和小刚分别在桥面上的A,B处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
 21. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
21. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:地铁站
A
B
C
D
E
x(千米)
8
9
10
11.5
13
y1(分钟)
18
20
22
25
28
(1)、求y1关于x的函数表达式;(2)、李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2= x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.22.
(1)、【探索发现】如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
 (2)、【拓展应用】
(2)、【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 . (用含a,h的代数式表示)
(3)、【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
(4)、【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
23. 如图,抛物线y=ax2+bx+3经过点 B(-1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t. (1)、求抛物线的表达式;(2)、过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)(3)、在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;(4)、在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)(3)、在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;(4)、在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.