山西省阳泉市平定县2015-2016九年级上学期数学期末考试试卷

试卷更新日期：2018-05-23 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程（x+6）²=16可转化为两个一元一次方程，其中一个一元一次方程是x+6=4，则另一个一元一次方程是（）

A、x-6=-4 B、x-6=4 C、x+6=4 D、x+6=-4

查看试题解析
2. 下列一元二次方程有两个相等实数根的是（）

A、x²+3=0 B、x²+2x=0 C、（x+1）²=0 D、（x+3）（x-1）=0

查看试题解析
3. 把抛物线y=-2x²先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为（）

A、y=-2（x+1）²+2 B、y=-2（x+1）²-2 C、y=-2（x-1）²+2 D、y=-2（x-1）²-2

查看试题解析
4. 学校组织校外实践活动，安排给九年级三辆车，小明与小红都可以从这三辆车中任选一辆搭乘，小明与小红同车的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
5. 如图，已知△ABC的三个顶点均在格点上，则cosA的值为（）

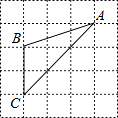A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
6. 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁ ， l₂ ， l₃于点A，B，C；直线DF分别交l₁ ， l₂ ， l₃于点D，E，F．AC与DF相交于点H，且AH=2，HB=1，BC=5，则 $\frac{D E}{E F}$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
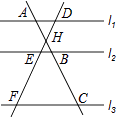7. 如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为（）

A、45° B、50° C、60° D、75°

查看试题解析
8.
如图，斜面AC的坡度（CD与AD的比）为1：2，AC=3 $\sqrt{5}$ 米，坡顶有旗杆BC，旗杆顶端B点与A点有一条彩带相连．若AB=10米，则旗杆BC的高度为（）

A、5米 B、6米 C、8米 D、（3+ $\sqrt{5}$ ）米

查看试题解析
9. 如图，正比例函数y₁=k₁x的图象与反比例函数y₂= $\frac{k_{2}}{x}$ 的图象相交于A，B两点，其中点A的横坐标为2，当y₁＞y₂时，x的取值范围是（）

A、x＜-2或x＞2 B、x＜-2或0＜x＜2 C、-2＜x＜0或0＜x＜2 D、-2＜x＜0或x＞2

查看试题解析
10. 如图，已知▱ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为（）

A、130° B、150° C、160° D、170°

查看试题解析

二、填空题

11. 方程3(x－5)²=2(x－5)的根是

查看试题解析
12. 二次函数y=x²-2x-3的图象如图所示．当y＜0时，自变量x的取值范围是．

查看试题解析
13. 一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗，每次随机摸出一颗珠子，放回摇匀后再摸，通过多次试验发现摸到白珠子的频率稳定在0.3左右，则盒子中黑珠子可能有颗．

查看试题解析
14. 一个容器盛满纯药液40L，第一次倒出若干升后，用水加满；第二次又倒出同样体积的溶液，这时容器里只剩下纯药液10L，则每次倒出的液体是L．

查看试题解析
15. 如图，在△ABC中，∠A=30°，∠B=45°，AC= $2 \sqrt{3}$ ，则AB的长为．

查看试题解析
16. 如图，Rt△AOB的一条直角边OB在x轴上，双曲线y= $\frac{k}{x}$ （x>0）经过斜边OA的中点C，与另一直角边交于点D．若S_△_OCD=9，则S_△_OBD的值为．

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{12} + 2^{- 1} - 4 \cos 30 ° + | - \cos 60 ° |$

(2)、用配方法解方程：4x²-8x-5=0．

查看试题解析
18. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点三角形ABC（顶点是网格线的交点）．

(1)、先将△ABC竖直向上平移6个单位，再水平向右平移3个单位得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

(2)、将△A₁B₁C₁绕B₁点顺时针旋转90°，得△A₂B₁C₂ ，请画出△A₂B₁C₂；

(3)、线段B₁C₁变换到B₁C₂的过程中扫过区域的面积为．

查看试题解析
19. 如图，在Rt△BAD中，延长斜边BD到点C，使DC= $\frac{1}{2} B D$ ，连接AC，若tanB= $\frac{5}{3}$ ，求tan∠CAD的值．

查看试题解析
20. 为了参加中考体育测试，甲、乙、丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传给其余两人的机会是均等的，由甲开始传球，共传球三次．

(1)、请利用树状图列举出三次传球的所有可能情况；

(2)、求三次传球后，球回到甲脚下的概率；

(3)、三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？

查看试题解析
21. 如图，在平面直角坐标系xOy中，一次函数y $_{_{1}}$ =ax+b（a，b为常数，且a≠0）与反比例函数y $_{2}$ = $\frac{m}{x}$ （m为常数，且m≠0）的图象交于点A（-2，1）、B（1，n）．

(1)、求反比例函数和一次函数的解析式；

(2)、连结OA、OB，求△AOB的面积；

(3)、直接写出当y₁＜y₂＜0时，自变量x的取值范围．

查看试题解析
22. 如图，海中一小岛上有一个观测点A，某天上午9：00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行．当天上午9：30观测到该渔船在观测点A的北偏西60°方向上的C处．若该渔船的速度为每小时30海里，在此航行过程中，问该渔船从B处开始航行多少小时，离观测点A的距离最近？（计算结果用根号表示，不取近似值）．

查看试题解析
23. 操作与证明：
如图1，已知P是矩形ABCD的边BC上的一个点（P与B、C两点不重合），过点P作射线PE⊥AP，在射线PE上截取线段PF，使得PF=AP．

(1)、过点F作FG⊥BC交射线BC点G．（尺规作图，保留痕迹，不写作法）

(2)、求证：FG=BP．
探究与计算：

(3)、如图2，若AB=BC，连接CF，求∠FCG的度数；

(4)、在（3）的条件下，当 $\frac{B P}{B C}$ = $\frac{3}{4}$ 时，求sin∠CFP的值．

查看试题解析
24. 综合与探究：如图，抛物线y=- $\frac{1}{4}$ x²+bx+c与x轴交于A（-1，0），B（5，0）两点，过点B作线段BC⊥x轴，交直线y=-2x于点C．

(1)、求该抛物线的解析式；

(2)、求点B关于直线y=-2x的对称点B′的坐标，判定点B′是否在抛物线上，并说明理由；

(3)、点P是抛物线上一动点，过点P作y轴的平行线，交线段B′C于点D，是否存在这样的点P，使四边形PBCD是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析