山西省太原市2015-2016学年九年级上学期数学期末考试试卷
试卷更新日期:2018-05-23 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,反比例函数y= 的图象位于( )A、第二、四象限 B、第一、三象限 C、第一、四象限 D、第三、四象限2. 若 ,则 等于( )A、 B、 C、 D、3. 一个圆柱体钢块,从正中间挖去一个长方体得到的零件毛坯的俯视图如图,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、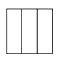 4. 校运动会上甲、乙、丙、丁四名选手参加100米决赛,赛场有1号、2号、3号、4号4条跑道.如果选手以随机抽签的方式决定各自的跑道,则甲抽到1号跑道,乙抽到2号跑道的概率是( )A、 B、 C、 D、5. 已知△ABC∽△ ,△ 的面积为6 ,周长为△ABC周长的一半,则△ABC的面积等于( )A、1.5 B、3 C、12 D、246.
4. 校运动会上甲、乙、丙、丁四名选手参加100米决赛,赛场有1号、2号、3号、4号4条跑道.如果选手以随机抽签的方式决定各自的跑道,则甲抽到1号跑道,乙抽到2号跑道的概率是( )A、 B、 C、 D、5. 已知△ABC∽△ ,△ 的面积为6 ,周长为△ABC周长的一半,则△ABC的面积等于( )A、1.5 B、3 C、12 D、246.如图,晚上小明由甲处径直走到乙处的过程中,他在路灯M下的影长在地面上的变化情况是( )
 A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长7. 若A(3,y1),B(2,y2)在函数y= 的图象上,则y1 , y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定8. 从一块正方形铁皮的四角上各剪去一个边长为3cm的小正方形,制成一个无盖的盒子,若盒子的容积为300cm3 , 则铁皮的边长为( )A、16cm B、14cm C、13cm D、11cm9. 一次函数 与反比例函数 在同一平面直角坐标系中的图象可能是( )A、
A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长7. 若A(3,y1),B(2,y2)在函数y= 的图象上,则y1 , y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定8. 从一块正方形铁皮的四角上各剪去一个边长为3cm的小正方形,制成一个无盖的盒子,若盒子的容积为300cm3 , 则铁皮的边长为( )A、16cm B、14cm C、13cm D、11cm9. 一次函数 与反比例函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、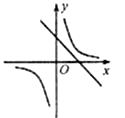 C、
C、 D、
D、
二、填空题
-
10. 已知 是方程 的一个根,则c的值是.11. 如图,已知直线 ,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为cm.
 12. 一个不透明的袋子中有1个白球、3个黄球和2个红球,这些球除颜色外都相同.将袋子中的球搅拌均匀,从中一次随机摸出两个球都是黄球的概率为.13. 将一副三角尺按如图所示的方式叠放在一起,边AD不BC相交不点E,则 的值等于.
12. 一个不透明的袋子中有1个白球、3个黄球和2个红球,这些球除颜色外都相同.将袋子中的球搅拌均匀,从中一次随机摸出两个球都是黄球的概率为.13. 将一副三角尺按如图所示的方式叠放在一起,边AD不BC相交不点E,则 的值等于. 14. 如图所示是反比例函数y= 与y=- 在x轴上方的图象,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上运动,则△ABP的面积等于.
14. 如图所示是反比例函数y= 与y=- 在x轴上方的图象,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上运动,则△ABP的面积等于.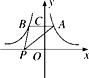 15. 如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点 处,此时点 落在点 处.已知折痕EF=13,则AE的长等于.
15. 如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点 处,此时点 落在点 处.已知折痕EF=13,则AE的长等于.
三、解答题
-
16. 解方程: .17. 如图,△ABC与△ 是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
 (1)、画出位似中心O;(2)、△ABC与△ 的相似比为 , 面积比为18. 如图,在▱ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求BC的长.
(1)、画出位似中心O;(2)、△ABC与△ 的相似比为 , 面积比为18. 如图,在▱ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求BC的长. 19. 晚上,小亮在广场上乘凉.中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照亮灯.知小亮的身高1.6m.
19. 晚上,小亮在广场上乘凉.中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照亮灯.知小亮的身高1.6m. (1)、图中画出小亮在照明灯P照射下的影子BC;(2)、如果灯杆高PO=12m,小亮不灯杆的距离BO=13m,求小亮影子BC的长度.20. 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P,Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值.
(1)、图中画出小亮在照明灯P照射下的影子BC;(2)、如果灯杆高PO=12m,小亮不灯杆的距离BO=13m,求小亮影子BC的长度.20. 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P,Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值. 21. 数学活动——探究特殊的平行四边形.
21. 数学活动——探究特殊的平行四边形.问题情境:
如图,在四边形ABCD中,AC为对角线,AB=AD,BC=DC.请你添加条件,使它们成为特殊的平行四边形.
提出问题:
 (1)、第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;(2)、第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.22. 说明:从(A),(B)两题中任选一题作答.
(1)、第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;(2)、第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.22. 说明:从(A),(B)两题中任选一题作答.春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售出20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件应定价为多少元?
我选择: ▲
23. 说明:在解答“结论应用”时,从A,B两题中任选一题作答.问题探究:
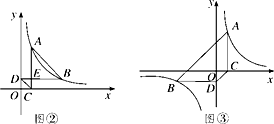
启知学习小组在课外学习时,发现了这样一个问题:如图①,在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图①中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
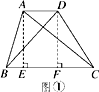
结论应用:
在平面直角坐标系中,反比例函数y= (x≠0)的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
 (1)、A
(1)、AⅠ.求反比例函数的表达式;
Ⅱ.如图②,已知b=1,AC,BD相交于点E,求证:CD∥AB.
(2)、BⅠ.求反比例函数的表达式;
Ⅱ.如图③,若点B在第三象限,判断并证明CD与AB的位置关系.