2018年浙江省湖州市中考数学冲刺模拟卷(2)
试卷更新日期:2018-05-23 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、 B、 C、3 D、-32. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
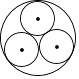 B、
B、 C、
C、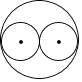 D、
D、 3. 如图是一个几何体的三视图,则这个几何体是( )
3. 如图是一个几何体的三视图,则这个几何体是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. “2014年至2016年,中国同‘一带一路’沿线国家贸易总额超过3万亿美元”,将数据3万亿美元用科学记数法表示为( )A、3×1014美元 B、3×1013美元 C、3×1012美元 D、3×1011美元5. 一组数据3、5、8、3、4的众数与中位数分别是( )
4. “2014年至2016年,中国同‘一带一路’沿线国家贸易总额超过3万亿美元”,将数据3万亿美元用科学记数法表示为( )A、3×1014美元 B、3×1013美元 C、3×1012美元 D、3×1011美元5. 一组数据3、5、8、3、4的众数与中位数分别是( )
A、3,8 B、3,3 C、3,4 D、4,36. 下列命题是真命题的是( )A、相等的角是对顶角 B、若实数a,b满足a2=b2 , 则a=b C、若实数a,b满足a<0,b<0,则ab<0 D、角的平分线上的点到角的两边的距离相等7. 分别写有数字 0,-3,-4,2,5 的五张卡片,除数字不同外其他均相同,从中任抽一张, 那么抽到非负数的概率是( )
A、 B、 C、 D、8. 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( ) A、70° B、50° C、45° D、20°9. 我们定义一种变换§:对于一个由5个数组成的数列S1 , 将其中的每个数换成该数在S1中出现的次数,可得到一个新数列S2 . 例如:当数列S1是 (4,2,3,4,2)时,经过变换§可得到的新数列S2是(2,2,1,2,2).若数列S1可以由任意5个数组成,则下列的数列可作为S2的是( )A、(1,2,1,2,2) B、(2,2,2,3,3) C、(1,1,2,2,3) D、(1,2,1,1,2)10. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A、70° B、50° C、45° D、20°9. 我们定义一种变换§:对于一个由5个数组成的数列S1 , 将其中的每个数换成该数在S1中出现的次数,可得到一个新数列S2 . 例如:当数列S1是 (4,2,3,4,2)时,经过变换§可得到的新数列S2是(2,2,1,2,2).若数列S1可以由任意5个数组成,则下列的数列可作为S2的是( )A、(1,2,1,2,2) B、(2,2,2,3,3) C、(1,1,2,2,3) D、(1,2,1,1,2)10. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( ) A、5 B、4 C、 D、
A、5 B、4 C、 D、二、填空题
-
11. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 .
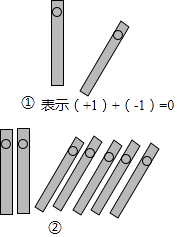 12. 分式方程 的解为 .13. 如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF= .
12. 分式方程 的解为 .13. 如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF= .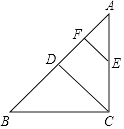 14.
14.如图,AC⊥BC于点C,CD⊥AB于点D,其中长度能表示点到直线(或线段)的距离的线段有 条.
 15. 在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为.16. 正比例函数y1=mx(m>0)的图象与反比例函数y2= (k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是 .
15. 在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为.16. 正比例函数y1=mx(m>0)的图象与反比例函数y2= (k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是 .三、解答题
-
17. 计算:tan60°+| ﹣2|+( )﹣1﹣(π+2)0 .18. 先化简,后求值: ,其中 , .19. 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB= ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
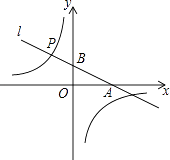 (1)、求直线l的表达式;(2)、若反比例函数y= 的图象经过点P,求m的值.20.
(1)、求直线l的表达式;(2)、若反比例函数y= 的图象经过点P,求m的值.20.如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°.
(1)求∠OBA的度数;
(2)求∠D的度数.
 21.
21.某学校要了解学生上学交通情况,选取九年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知九年级乘公交车上学的人数为50人.
 (1)、九年级学业生中,骑自行车和乘公交车上学哪个更多?多多少人?(2)、如果全校有学生2000人,学校准备的400个自行车停车位是否足够?22. 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
(1)、九年级学业生中,骑自行车和乘公交车上学哪个更多?多多少人?(2)、如果全校有学生2000人,学校准备的400个自行车停车位是否足够?22. 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.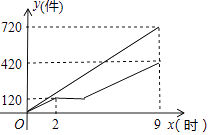 (1)、甲车间每小时加工服装件数为件;这批服装的总件数为件.
(1)、甲车间每小时加工服装件数为件;这批服装的总件数为件.
(2)、求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;(3)、求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.23.如图1,直线y=x+1与抛物线y=2x2相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
 (1)、①求A、B的坐标;②求证:∠ANM=∠BNM;(2)、如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线y=2x2变为y=ax2(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.24. 如图(1)正方形ABCD和正方形AEFG,边AE在边AB上,AB=12,AE=6 .将正方形AEFG绕点A逆时针旋转α(0°≤α≤45°)
(1)、①求A、B的坐标;②求证:∠ANM=∠BNM;(2)、如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线y=2x2变为y=ax2(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.24. 如图(1)正方形ABCD和正方形AEFG,边AE在边AB上,AB=12,AE=6 .将正方形AEFG绕点A逆时针旋转α(0°≤α≤45°) (1)、如图(2)正方形AEFG旋转到此位置,求证:BE=DG;
(1)、如图(2)正方形AEFG旋转到此位置,求证:BE=DG;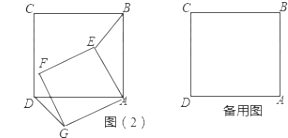 (2)、在旋转的过程中,当∠BEA=120°时,试求BE的长;(3)、BE的延长线交直线DG于点Q,当正方形AEFG由图(1)绕点A逆时针旋转45°,请直接写出旋转过程中点Q运动的路线长;(4)、在旋转的过程中,是否存在某时刻BF=BC?若存在,试求出DQ的长;若不存在,请说明理由.(点Q即(3)中的点)
(2)、在旋转的过程中,当∠BEA=120°时,试求BE的长;(3)、BE的延长线交直线DG于点Q,当正方形AEFG由图(1)绕点A逆时针旋转45°,请直接写出旋转过程中点Q运动的路线长;(4)、在旋转的过程中,是否存在某时刻BF=BC?若存在,试求出DQ的长;若不存在,请说明理由.(点Q即(3)中的点)