山西省农大附中2015-2016学年九年级上学期数学期末考试试卷
试卷更新日期:2018-05-23 类型:期末考试
一、单选题
-
1. 关于x的方程 的解为( )A、 , B、 , C、 , D、 ,2. 下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图所示,点A,B,C在圆O上,∠A=64°,则∠BOC的度数是( )
3. 如图所示,点A,B,C在圆O上,∠A=64°,则∠BOC的度数是( ) A、26° B、116° C、128° D、154°4.
A、26° B、116° C、128° D、154°4.如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角形个数是( )
 A、1 B、2 C、3 D、45. 随机闭合开关K1,K2,K3中的两个,则能让两盏灯泡同时发光的概率为( )
A、1 B、2 C、3 D、45. 随机闭合开关K1,K2,K3中的两个,则能让两盏灯泡同时发光的概率为( ) A、 B、 C、 D、6. 已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标分别变成原来的2倍,得到点A′,B′,C′。下列说法正确的是( )A、△A′B′C′与△ABC是位似图形,位似中心是点(1,0) B、△A′B′C′与△ABC是位似图形,位似中心是点(0,0) C、△A′B′C′与△ABC是相似图形,但不是位似图形 D、△A′B′C′与△ABC不是相似图形7. 在 的图象中,阴影部分面积不为1的是( )A、
A、 B、 C、 D、6. 已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标分别变成原来的2倍,得到点A′,B′,C′。下列说法正确的是( )A、△A′B′C′与△ABC是位似图形,位似中心是点(1,0) B、△A′B′C′与△ABC是位似图形,位似中心是点(0,0) C、△A′B′C′与△ABC是相似图形,但不是位似图形 D、△A′B′C′与△ABC不是相似图形7. 在 的图象中,阴影部分面积不为1的是( )A、 B、
B、 C、
C、 D、
D、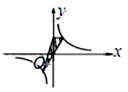 8. 如图所示,⊙O中,弦AB,CD相交于P点,则下列结论正确的是( )
8. 如图所示,⊙O中,弦AB,CD相交于P点,则下列结论正确的是( ) A、PA AB=PC PB B、PA PB=PC PD C、PA AB=PC CD D、PA∶PB=PC∶PD9. 如图,正比例函数y1与反比例函数y2相交于点E(﹣1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是( )
A、PA AB=PC PB B、PA PB=PC PD C、PA AB=PC CD D、PA∶PB=PC∶PD9. 如图,正比例函数y1与反比例函数y2相交于点E(﹣1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是( )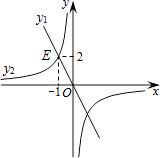 A、
A、 B、
B、 C、
C、 D、
D、 10. 函数 与 在同一直角坐标系中的图象可能是( )A、
10. 函数 与 在同一直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如图,直线 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是。
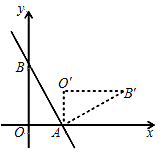 12. 二次函数 的图象的顶点与原点的距离为5,则c=。13. 在比例尺1∶6000000的地图上,量得南京到北京的距离是15cm,这两地的实际距离是km。14. 从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
12. 二次函数 的图象的顶点与原点的距离为5,则c=。13. 在比例尺1∶6000000的地图上,量得南京到北京的距离是15cm,这两地的实际距离是km。14. 从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
根据以上数据可以估计,该玉米种子发芽的概率约为。(精确到0.1)
15. 已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF=。 16. 如图,反比例函数 (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6)。若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是。
16. 如图,反比例函数 (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6)。若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是。
三、解答题
-
17. 在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
 (1)、请估计当n很大时,摸到白球的频率将会接近;(精确到0.1)(2)、假如你摸一次,你摸到白球的概率P(白球)=;(3)、试估算盒子里黑、白两种颜色的球各有多少个?18. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2)。
(1)、请估计当n很大时,摸到白球的频率将会接近;(精确到0.1)(2)、假如你摸一次,你摸到白球的概率P(白球)=;(3)、试估算盒子里黑、白两种颜色的球各有多少个?18. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2)。 (1)、画出△ABC关于y轴对称的 ;
(1)、画出△ABC关于y轴对称的 ;
(2)、画出△ABC关于原点O成中心对称的 。
19. 如图所示,在△ABC中,已知DE∥BC。 (1)、△ADE与△ABC相似吗?为什么?
(1)、△ADE与△ABC相似吗?为什么?
(2)、它们是位似图形吗?如果是,请指出位似中心。20. 某商店准备购进一批季节性小家电,单价40元,经市场预测,销售定价为52元时,可售出180个。定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个。因受库存的影响,每批次进货个数不得超过180个。商店若准备获利2000元,则应进货多少个?定价多少元?
21. 如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D。连接AC,若BC=6,DE=1,求AC的长。 22. 为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示)。现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?
22. 为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示)。现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?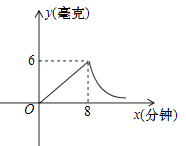 23. 如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。
23. 如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。 (1)、求证:△ABE∽△ECF;
(1)、求证:△ABE∽△ECF;
(2)、找出与△ABH相似的三角形,并证明;
(3)、若E是BC中点,BC=2AB,AB=2,求EM的长。
24. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知 ,OE=3AE,点B的坐标为(m, )。 (1)、求反比例函数的解析式。(2)、求一次函数的解析式。(3)、在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标。
(1)、求反比例函数的解析式。(2)、求一次函数的解析式。(3)、在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标。