2018年浙江省湖州市中考数学冲刺模拟卷(1)
试卷更新日期:2018-05-23 类型:中考模拟
一、选择题
-
1. 下列各数中是无理数的是( )A、 B、 C、 D、2. 将△ABC的各点的横坐标都加上3,纵坐标不变,所得图形与原图形相比( )A、向右平移了3个单位 B、向左平移了3个单位 C、向上平移了3个单位 D、向下平移了3个单位3. 在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )A、 B、 C、 D、4. 不等式组 的解集是( )A、x<﹣1 B、x<3 C、x>3 D、﹣1<x<35. 为了参加中学生篮球运动会,某校篮球队准备购买10双运动鞋,经统计10双运动鞋尺码(cm)如表所示:
尺码
25
25.5
26
26.5
27
购买量(双)
2
4
2
1
1
则这10双运动鞋的众数和中位数分别为( )
A、25.5 cm 26 cm B、26 cm 25.5 cm C、26 cm 26 cm D、25.5 cm 25.5 cm6. 如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )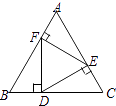 A、1:3 B、2:3 C、 :2 D、 :37. 在我校读书月活动中,小玲在书城买了一套科普读物,有上、中、下三册,要整齐的摆放在书架上,恰好摆成“上、中、下”顺序的概率是( )A、 B、 C、 D、8. 如图,一个几何体的主视图和左视图都是底边长为6,高为4的等腰三角形,俯视图是一个圆,那么这个几何体的侧面积是( )
A、1:3 B、2:3 C、 :2 D、 :37. 在我校读书月活动中,小玲在书城买了一套科普读物,有上、中、下三册,要整齐的摆放在书架上,恰好摆成“上、中、下”顺序的概率是( )A、 B、 C、 D、8. 如图,一个几何体的主视图和左视图都是底边长为6,高为4的等腰三角形,俯视图是一个圆,那么这个几何体的侧面积是( ) A、12π B、24π C、 π D、15π9.
A、12π B、24π C、 π D、15π9.如图,直角三角形ABC的两直角边BC=12,AC=16,则△ABC的斜边AB上的高CD的长是( )。
 A、20 B、10 C、9.6 D、810.
A、20 B、10 C、9.6 D、810.在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , ………按这样的规律进行下去,第2012个正方形的面积为( )
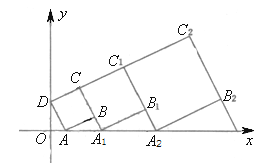 A、5()2010 B、5()2010 C、5()2012 D、5()4022
A、5()2010 B、5()2010 C、5()2012 D、5()4022二、填空题
-
11. 分解因式:x2﹣5x= .12. 要使分式有意义,那么x应满足的条件是 .13. 如果一个正多边形每一个内角都等于144°,那么这个正多边形的边数是 .14. 等腰三角形一腰长为5,一边上的高为3,则底边长为 .
15. 如图,PA、PB是⊙O的切线,切点分别是A、B,若∠APB=60°,PA=3.则⊙O的半径是 。
16. 如图,在平面直角坐标系中,▱ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣ (x<0)与y= (x>0)的图象上,则▱ABCD的面积为 .
三、解答题
-
17. 计算:﹣22++(3+π)0﹣|﹣3|.18. 解方程: ﹣ =1.19. 关于x,y方程组 的解满足x>0,求m的取值范围.20.
新学期开学初,王刚同学对部分同学暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
时间分组
0.5~20.5
20.5~40.5
40.5~60.5
60.5~80.5
80.5~100.5
频 数
20
25
30
15
10
(1)王刚同学抽取样本的容量是多少?
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?
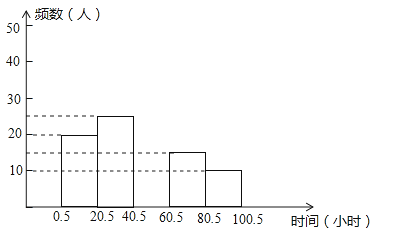 21.
21.如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(1)求证:CF为⊙O的切线.
(2)若半径ON⊥AD于点M,CE= , 求图中阴影部分的面积.
 22.
22.正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
 23.
23.如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
 (1)、当t为何值时,点Q与点D重合?(2)、当⊙Q经过点A时,求⊙P被OB截得的弦长.(3)、若⊙P与线段QC只有一个公共点,求t的取值范围.24.
(1)、当t为何值时,点Q与点D重合?(2)、当⊙Q经过点A时,求⊙P被OB截得的弦长.(3)、若⊙P与线段QC只有一个公共点,求t的取值范围.24.已知,如图,过点E(0,-1)作平行于
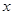 轴的直线 , 抛物线上的两点A、B的横坐标分别为
轴的直线 , 抛物线上的两点A、B的横坐标分别为 1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF,DF.
1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF,DF.
(1)求点A,B,F的坐标;
(2)求证:;
(3)点是抛物线对称轴右侧图象上的一动点,过点P作交X轴于点Q,是否存在点P使得与相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.