备考2018年数学中考冲刺卷05(深圳专版)
试卷更新日期:2018-05-23 类型:中考模拟
一、选择题
-
1. 有理数﹣ 的相反数的倒数是( )A、﹣ B、﹣ C、 D、2. 光的速度约为30万公里每秒,30万用科学记数法表示为( )
A、3×105 B、3×106 C、3×107 D、3×1083. 下列运算正确的是( )A、2a3•a4=2a7 B、a3+a4=a7 C、(2a4)3=8a7 D、a3÷a4=a4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图所示的四个几何体,其中左视图与俯视图相同的几何体共有几个( )
5. 如图所示的四个几何体,其中左视图与俯视图相同的几何体共有几个( ) A、1 B、2 C、3 D、46. 近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
A、1 B、2 C、3 D、46. 近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班学生的成绩统计如下:成绩(分)
60
70
80
90
100
人数
4
8
12
11
5
则该班学生成绩的众数和中位数分别是( )
A、70分,80分 B、80分,80分 C、90分,80分 D、80分,90分7. 设n为正整数,且n<<n+1,则n的值为( )A、5 B、6 C、7 D、88.已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax﹣2b与反比例函数y= 在同一平面直角坐标系中的图象大致是( )
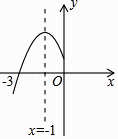 A、
A、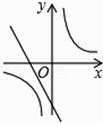 B、
B、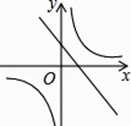 C、
C、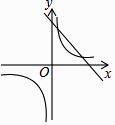 D、
D、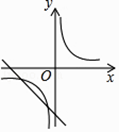 9. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
9. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )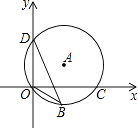 A、 B、 C、 D、10. 已知甲、乙两种商品的原价和为200元,因市场变化,甲商品降价10%,乙商品提高10%,调价后甲、乙两种商品的单价和比原单价和提高了5%,求甲、乙两种商品的原单价分别是( )A、50元,150元 B、150元,50元 C、80元,120元 D、120元,80元11.
A、 B、 C、 D、10. 已知甲、乙两种商品的原价和为200元,因市场变化,甲商品降价10%,乙商品提高10%,调价后甲、乙两种商品的单价和比原单价和提高了5%,求甲、乙两种商品的原单价分别是( )A、50元,150元 B、150元,50元 C、80元,120元 D、120元,80元11.如图,在 ABC中,AD平分 BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).
 A、2 B、4 C、6 D、812.
A、2 B、4 C、6 D、812.如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4 ,其中正确的结论个数为( )
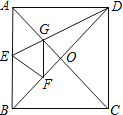 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 在实数范围内分解因式:4m2﹣16= .14. 一组数据1,3,2,5,x的平均数为3,那么这组数据的方差是 .15. 在一次猜数字游戏中,小红写出如下一组数:1, , , , …,小军猜想出的第六个数字是 ,也是正确的,根据此规律,第n个数是 .16.
如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=(x>0)的图象上,顶点A1、B1分别在x轴和y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y=(x>0)的图象上,顶点A2在x轴的正半轴上,则P2点的坐标为 ,P3的坐标为 .

三、解答题
-
17. 计算:( )﹣1﹣6cos30°﹣( )0+ .18. 解分式方程: + = .19.
某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院,B.小小数学家,C.小小外交家,D.未来科学家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有多少人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好同时选中甲、乙两位同学的概率(用树状图或列表法解答).
 20. 如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600米到达B处,测得C在点B的北偏西60°方向上.
20. 如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600米到达B处,测得C在点B的北偏西60°方向上. (1)、MN是否穿过原始森林保护区,为什么?(参考数据: ≈1.732)(2)、若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?21. 某班将举行“防溺水安全知识竞赛”活动,班主任安排班长购买奖品,下面是班长买回奖品时与班主任的对话情况:
(1)、MN是否穿过原始森林保护区,为什么?(参考数据: ≈1.732)(2)、若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?21. 某班将举行“防溺水安全知识竞赛”活动,班主任安排班长购买奖品,下面是班长买回奖品时与班主任的对话情况:班长:买了两种不同的奖品共50件,单价分别为3元和5元,我领了200元,现在找回35元
班主任:你肯定搞错了!
班长:哦!我把自己口袋里的15元一起当作找回的钱款了.
班主任:这就对了!
请根据上面的信息,解决下列问题:
(1)、计算两种奖品各买了多少件?(2)、请你解释:班长为什么不可能找回35元?22. 如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8. (1)、求证:DF是⊙O的切线;(2)、求证:OC2=OE•OP;(3)、求线段EG的长.23. 如图,在平面直角坐标系中,抛物线 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)、求证:DF是⊙O的切线;(2)、求证:OC2=OE•OP;(3)、求线段EG的长.23. 如图,在平面直角坐标系中,抛物线 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.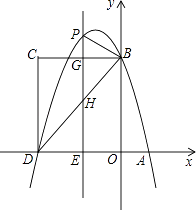 (1)、求该抛物线的解析式;(2)、当点P在直线BC上方时,请用含m的代数式表示PG的长度;(3)、在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、当点P在直线BC上方时,请用含m的代数式表示PG的长度;(3)、在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.