备考2018年数学中考冲刺卷04(深圳专版)
试卷更新日期:2018-05-23 类型:中考模拟
一、选择题
-
1. |-2|的相反数是 ( )A、 B、-2 C、 D、22
-
2. 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
3. 李克强总理在2017年政府工作报告中指出:“完善就业政策,加大就业培训力度,加强对灵活就业、新就业形态的支持,今年高校毕业生7950000人,再创历史新高,要实施好就业促进、创业引领、基层成长等计划,促进多渠道就业创业.”其中数据7950000用科学记数法表示是( )A、795×104 B、7.95×105 C、0.795×107 D、7.95×106
-
4. 下列图形中,既是中心对称,又是轴对称图形的是( )A、
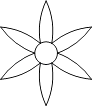 B、
B、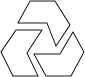 C、
C、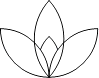 D、
D、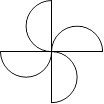
-
5. 下列说法不正确的是( )A、过任意一点可作已知直线的一条平行线 B、在同一平面内两条不相交的直线是平行线 C、在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D、直线外一点与直线上各点连接的所有线段中,垂线段最短
-
6. 一元一次不等式组 的解集是( )A、 B、 C、 D、 或
-
7. 某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )A、不赔不赚 B、赚了32元 C、赔了8元 D、赚了8元
-
8. 下列作图语句正确的是( )A、延长线段AB到C,使AB=BC B、延长射线AB C、过点A作AB∥CD∥EF D、作∠AOB的平分线OC
-
9. 下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③三角形的一个外角大于任何一个内角.
④如果x2>0,那么x>0.
A、1个 B、2个 C、3个 D、4个 -
10. 在暑假到来之前,某机构向八年级学生推荐了A,B,C三条游学线路,现对全级学生喜欢哪一条游学线路作调查,以决定最终的游学线路,下面的统计量中最值得关注的是( )A、方差 B、平均数 C、中位数 D、众数
-
11. 如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.( )
 A、40 B、60﹣20 C、20 D、20
A、40 B、60﹣20 C、20 D、20 -
12. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 = ,则S△EDH=13S△CFH .
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
13. 分解因式:5x3﹣10x2+5x= .
-
14. 甲、乙、丙三人玩“丢飞碟”游戏,飞碟从一人传到另一人记为丢一次,若从乙开始,则丢两次后,飞碟传到丙处的概率为 .
-
15. 已知a+b=3,ab=2,则a2+b2的值为 .
-
16. 如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7 ,则EF的长为 .

三、解答题
-
17. 计算:|2﹣tan60°|﹣(π﹣3.14)0+(-)﹣2+ .
-
18. 先化简,再求值:( +2﹣x)÷ ,其中x满足x2+2x﹣3=0.
-
19. 在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
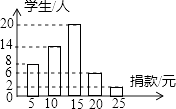 (1)、这50名同学捐款的众数为元,中位数为元;(2)、求这50名同学捐款的平均数;(3)、该校共有600名学生参与捐款,请估计该校学生的捐款总数.
(1)、这50名同学捐款的众数为元,中位数为元;(2)、求这50名同学捐款的平均数;(3)、该校共有600名学生参与捐款,请估计该校学生的捐款总数. -
20.
已知:如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P从点B出发,沿BC向点C匀速运动,速度为1cm/s;过点P作PD∥AB,交AC于点D,同时,点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动,连接PQ.设运动时间为t(s)(0<t<2.5),解答下列问题:
 (1)、当t为何值时,四边形ADPQ为平行四边形?(2)、设四边形ADPQ的面积为y(cm2),试确定y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使S四边形ADPQ:S△PQB=13:2?若存在,请说明理由,若存在,求出t的值,并求出此时PQ的距离.
(1)、当t为何值时,四边形ADPQ为平行四边形?(2)、设四边形ADPQ的面积为y(cm2),试确定y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使S四边形ADPQ:S△PQB=13:2?若存在,请说明理由,若存在,求出t的值,并求出此时PQ的距离. -
21. 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.
 (1)、求反比例函数的解析式;(2)、若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
(1)、求反比例函数的解析式;(2)、若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标. -
22.
如图在平面直角坐标系中,直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点P、Q同时从点A出发,运动时间为t秒.其中点P沿射线AB运动,速度为每秒4个单位长度,点Q沿射线AO运动,速度为每秒5个单位长度.以点Q为圆心,PQ长为半径作⊙Q.
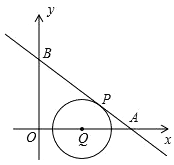 (1)、求证:直线AB是⊙Q的切线;(2)、过点A左侧x轴上的任意一点C(m,0),作直线AB的垂线CM,垂足为M.若CM与⊙Q相切于点D,求m与t的函数关系式(不需写出自变量的取值范围);(3)、在(2)的条件下,是否存在点C,直线AB、CM、y轴与⊙Q同时相切?若存在,请直接写出此时点C的坐标;若不存在,请说明理由.
(1)、求证:直线AB是⊙Q的切线;(2)、过点A左侧x轴上的任意一点C(m,0),作直线AB的垂线CM,垂足为M.若CM与⊙Q相切于点D,求m与t的函数关系式(不需写出自变量的取值范围);(3)、在(2)的条件下,是否存在点C,直线AB、CM、y轴与⊙Q同时相切?若存在,请直接写出此时点C的坐标;若不存在,请说明理由. -
23.
矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
 (1)、求AD的长;(2)、求阴影部分的面积和直线AM的解析式;(3)、求经过A、B、D三点的抛物线的解析式;(4)、在抛物线上是否存在点P,使S△PAM=?若存在,求出P点坐标;若不存在,请说明理由.
(1)、求AD的长;(2)、求阴影部分的面积和直线AM的解析式;(3)、求经过A、B、D三点的抛物线的解析式;(4)、在抛物线上是否存在点P,使S△PAM=?若存在,求出P点坐标;若不存在,请说明理由.
