备考2018年数学中考冲刺卷02（深圳专版）

试卷更新日期：2018-05-23 类型：中考模拟

进入出卷网下载

一、选择题

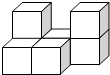
1. 在0， $| - 3 |$ ，－5，-3这四个数中，最大的数是（）

A、0 B、－3 C、 $| - 3 |$ D、－5

查看试题解析
2. 如图所示的图形是由7个完全相同的小正方体组成的立体图形，则下面四个平面图形中不是这个立体图形的三视图的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）

A、3x+2y=5xy B、4x﹣3x=1 C、ab﹣2ab=﹣ab D、2a+a=2a²

查看试题解析
4. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 某种病毒的直径约为0.0000000028米，该直径用科学记数法表示为（）

A、0.28×10^﹣⁸米 B、2.8×10^﹣¹⁰米 C、2.8×10^﹣⁹米 D、2.8×10^﹣⁸米

查看试题解析
6. 如图，∠MON=60°，且OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=4，则PQ的最小值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 一个不透明的布袋里装有若干个只有颜色不同的红球和白球，其中3个红球，且从布袋中随机摸出一个球，摸出的球是红球的概率是 $\frac{1}{3}$ ，则白球的个数是（）

A、6 B、7 C、8 D、9

查看试题解析
8. 已知下列命题：
①若a＞0，b＞0，则a+b＞0；
②若a²=b² ，则a=b；
③线段垂直平分线上的点到线段两端点距离相等；
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是（）

A、①③ B、②④ C、③④ D、②③

查看试题解析
9. 为保证达万高速公路在2012年底全线顺利通车，某路段规定在若干天内完成修建任务．已知甲队单独完成这项工程比规定时间多用10天，乙队单独完成这项工程比规定时间多用40天，如果甲、乙两队合作，可比规定时间提前14天完成任务．若设规定的时间为x天，由题意列出的方程是（）

A、 $\frac{1}{x - 10} + \frac{1}{x - 40} = \frac{1}{x + 14}$ B、 $\frac{1}{x + 10} + \frac{1}{x + 40} = \frac{1}{x - 14}$ C、 $\frac{1}{x + 10} - \frac{1}{x + 40} = \frac{1}{x - 14}$ D、 $\frac{1}{x - 10} - \frac{1}{x + 14} = \frac{1}{x - 40}$

查看试题解析
10. 在平面直角坐标系中，对于平面内任一点（m，n），规定以下两种变换①f（m，n）=（m，-n），如f（2，1）=（2，-1）；②g（m，n）= （-m，-n），如g（2，1）=（-2，-1）．按照以上变换有：f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（-3，2）]等于（）

A、（3，2） B、（3，-2） C、（-3，2） D、（-3，-2）

查看试题解析
11. 如图，以O为圆心的圆与直线y=﹣x+ $\sqrt{3}$ 交于A、B两点，若△OAB恰为等边三角形，则弧AB的长度为（）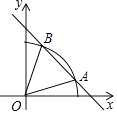

A、 $\frac{2}{3}$ π B、π C、 $\frac{\sqrt{2}}{3}$ π D、 $\frac{1}{3}$ π

查看试题解析
12.
如图，在边长为1的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），过点P作PM∥CD交BC于M点，PN∥BC交CD于N点，连接MN，在运动过程中，则下列结论：
①△ABE≌△BCF；②AE=BF；③AE⊥BF；④CF²=PE•BF；⑤线段MN的最小值为 $\frac{\sqrt{5} - 1}{2}$ ．
其中正确的结论有（）

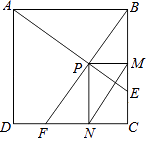A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 分解因式：x²﹣6xy+9y²= .

查看试题解析
14. 某学校规定学生的学期体育成绩有三部分组成：早锻炼及体育课外活动占10%，体育理论测试占30%，体育技能占60%．王明的三项成绩依次为90分，85分，90分，则王明学期的体育成绩是分．

查看试题解析
15. 若三角形的三边长分别为3，4，x﹣1，则x的取值范围是．

查看试题解析
16. 两个反比例函数y= $\frac{k}{x}$ （k＞1）和y= $\frac{1}{x}$ 在第一象限内的图象如图所示，点P在y= $\frac{k}{x}$ 的图象上，PC⊥x轴于点C，交y= $\frac{1}{x}$ 的图象于点A，PD⊥y轴于点D，交y= $\frac{1}{x}$ 的图象于点B，BE⊥x轴于点E，当点P在y= $\frac{k}{x}$ 图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化；④△OBA的面积等于四边形ACEB的面积．其中一定正确的是（填序号）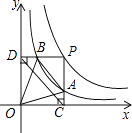

查看试题解析

三、解答题

17. 计算：（π﹣3.14）⁰+| $\sqrt{2}$ ﹣1|﹣（ $\frac{\sqrt{2}}{2}$ ）^﹣¹﹣2sin45°+（﹣1）²⁰¹⁶ ．

查看试题解析
18. 解不等式组： ${\begin{matrix} 9 x + 5 < 8 x + 7 \\ \frac{4}{3} x + 2 > 1 - \frac{2}{3} x \end{matrix}$ ，并写出其整数解．

查看试题解析
19.
为了解学生参加户外活动的情况，和谐中学对学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：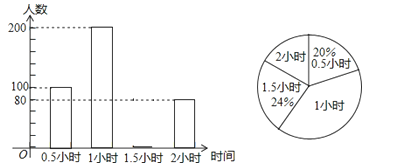
（1）求被抽样调查的学生有多少人？并补全条形统计图；
（2）每天户外活动时间的中位数是多少小时？
（3）该校共有1850名学生，请估计该校每天户外活动时间超过1小时的学生有多少人？

查看试题解析
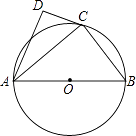
20. 如图，拦水坝的横断面为梯形ABCD，AB∥CD，坝顶宽DC为6米，坝高DG为2米，迎水坡BC的坡角为30°，坝底宽AB为（8+2 $\s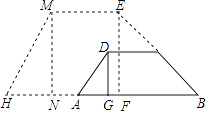qrt{3}$ ）米．

(1)、求背水坡AD的坡度；

(2)、为了加固拦水坝，需将水坝加高2米，并且保持坝顶宽度不变，迎水坡和背水坡的坡度也不变，求加高后坝底HB的宽度．

查看试题解析
21. 为了打造成渝之心区域交通枢纽，实现安岳县跨越式发展，我县外南街直通安岳大道建设正按投资计划有序推进，因道路建设需要开挖土石方，该建设工程队计划每小时挖掘土石方540方，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，已知该公司一台甲型挖掘机与一台乙型挖掘机每小时共挖土140方，5台甲型挖掘机与3台乙型挖掘机能恰好完成每小时的挖掘量．

(1)、求甲、乙两种型号的挖掘机每小时各挖土多少方？

(2)、若租用一台甲型挖掘机每小时100元，租用一台乙型挖掘机每小时120元，且每小时支付的总租金不超过850元，又恰好完成每小时的挖掘量，请设计该工程队的租用方案．

查看试题解析
22. 如图，AB是⊙O的直径，点C在⊙O上（异于A、B两点），AD⊥CD．
①若BC=3，AB=5，求AC的长？
②若AC是∠DAB的平分线，求证：直线CD与⊙O相切．

查看试题解析
23.
如图，矩形OABC的两边在坐标轴上，点A的坐标为（10，0），抛物线y=ax²+bx+4过点B，C两点，且与x轴的一个交点为D（﹣2，0），点P是线段CB上的动点，设CP=t（0＜t＜10）．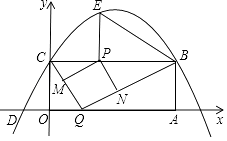

(1)、请直接写出B、C两点的坐标及抛物线的解析式；

(2)、过点P作PE⊥BC，交抛物线于点E，连接BE，当t为何值时，∠PBE=∠OCD？

(3)、点Q是x轴上的动点，过点P作PM∥BQ，交CQ于点M，作PN∥CQ，交BQ于点N，当四边形PMQN为正方形时，请求出t的值．

查看试题解析