备考2018年数学中考冲刺卷01(深圳专版)
试卷更新日期:2018-05-23 类型:中考模拟
一、选择题
-
1. 的相反数为( )A、2018 B、-2018 C、 D、2. 十八大以来,以习近平同志为核心的党中央把脱贫攻坚摆到治国理政的突出位置,2013﹣2017年这5年约有6600万人将脱贫,相当于一个法国的人口,将“6600万”这个数用科学记数法表示是( )A、6.6×103 B、6.6×107 C、6.6×108 D、6.6×10113. 下列图形中,可以是正方体表面展开图的是( )A、
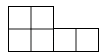 B、
B、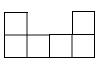 C、
C、 D、
D、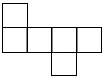 4. 不等式组 的解集为( )A、x<3 B、x≥2 C、2≤x<3 D、2<x<35. 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )A、平均数 B、中位数 C、众数 D、方差6. 不等式2x+3≥5的解集在数轴上表示正确的是( )
4. 不等式组 的解集为( )A、x<3 B、x≥2 C、2≤x<3 D、2<x<35. 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )A、平均数 B、中位数 C、众数 D、方差6. 不等式2x+3≥5的解集在数轴上表示正确的是( )
A、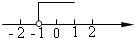 B、
B、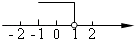 C、
C、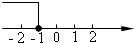 D、
D、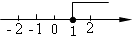 7. 一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
7. 一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( ) A、5L B、3.75L C、2.5L D、1.25L8. 一次函数 与二次函数 在同一直角坐标系中的图象可能是( )
A、5L B、3.75L C、2.5L D、1.25L8. 一次函数 与二次函数 在同一直角坐标系中的图象可能是( )
A、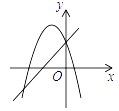 B、
B、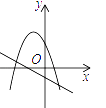 C、
C、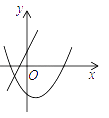 D、
D、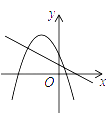 9. 如图,点A,B,C是⊙O上的点,∠AOB=70°,则∠ACB的度数是( )
9. 如图,点A,B,C是⊙O上的点,∠AOB=70°,则∠ACB的度数是( )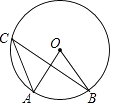 A、30° B、35° C、45° D、70°10. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A、30° B、35° C、45° D、70°10. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( ) A、
A、 B、
B、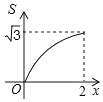 C、
C、 D、
D、 11. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= (k>0,x>0)的图象经过点C,则k的值为( )
11. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= (k>0,x>0)的图象经过点C,则k的值为( )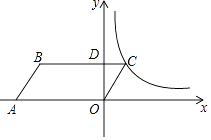 A、 B、 C、 D、12. 如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )
A、 B、 C、 D、12. 如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )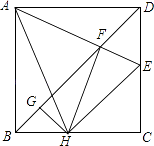 A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
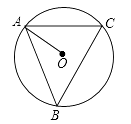
13. 分解因式:m2n﹣4mn+4n= .14. 若关于x的方程x2﹣6x+c=0有两个相等的实数根,则c的值为 .15. 穿越青海境内的兰馨高铁及大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,可列方程为 .16. 如图,已知⊙O是△ABC的外接圆,连接AO,若∠B=40°,则∠OAC=°.
三、解答题
-
17. 计算:( )﹣1﹣6cos30°﹣( )0+ .18. 先化简,再求值:( ﹣ )÷ ,其中a=2sin60°﹣tan45°.19. 某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别
次数x
频数(人数)
A
80≤x<100
6
B
100≤x<120
8
C
120≤x<140
m
D
140≤x<160
18
E
160≤x<180
6
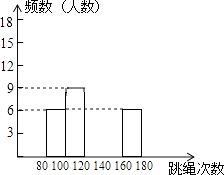
请结合图表解答下列问题:
(1)、表中的m=;(2)、请把频数分布直方图补完整;(3)、这个样本数据的中位数落在第组;(4)、若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.20. 如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( 取1.73,结果保留整数.)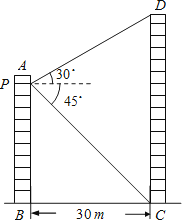 21.
21.甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
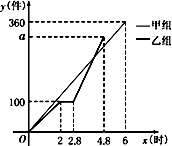 (1)、直接写出甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;22. 如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE.
(1)、直接写出甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;22. 如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE.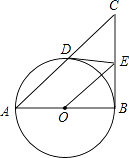 (1)、试判断OE与AC的关系,并说明理由;(2)、填空:
(1)、试判断OE与AC的关系,并说明理由;(2)、填空:①当∠BAC=时,四边形ODEB是正方形.
②当∠BAC=30°时, 的值为 .
23. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)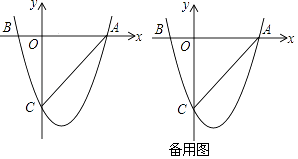 (1)、求该二次函数的解析式;
(1)、求该二次函数的解析式;
(2)、设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)、设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?