2018年浙江省杭州市中考数学冲刺模拟卷（3）

试卷更新日期：2018-05-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列运算中，正确的是( ）

A、 ${(- 2)}^{2} = - 4$ B、 $- 2^{2} = 4$ C、 $3^{2} = 6$ D、 ${(- 3)}^{3} = - 27$

查看试题解析
2. 据有关资料显示，2014年通过国家科技支撑计划，遵义市获得国家级科技专项重点项目资金5533万元，将5533万用科学记数法表示为（）．

A、 $5.533 \times 10^{8}$ B、 $5.533 \times 10^{7}$ C、 $5.533 \times 10^{6}$ D、 $55.33 \times 10^{6}$

查看试题解析
3. 如图，在△ABC中，DE∥BC，若AD=1，BD=2，则 $\frac{D E}{B C}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
4. 如图，数轴上的点A所表示的数为k，化简|k|+|1﹣k|的结果为（）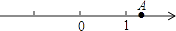

A、1 B、2k﹣1 C、2k+1 D、1﹣2k

查看试题解析
5. 下列运用等式的性质，变形不正确的是（）

A、若x=y，则x+5=y+5 B、若a=b，则ac=bc C、若 $\frac{a}{c}$ = $\frac{b}{c}$ ，则a=b D、若x=y，则 $\frac{x}{a} = \frac{y}{a}$

查看试题解析
6. 若a＜0，则下列不等关系错误的是（）

A、a＋5＜a＋7 B、5a＞7a C、5－a＜7－a D、 $\frac{a}{5}$ ＞ $\frac{a}{7}$

查看试题解析
7. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1892张照片，如果全班有x名同学，根据题意，列出方程为（）

A、x(x+1)=1892 B、x(x-1)=1892x2 C、x(x-1)=1892 D、2x(x+1)=1892

查看试题解析
8. 如图，在Rt△ABC中，AC=5cm，BC=12cm，∠ACB=90°，把Rt△ABC所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为（）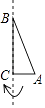

A、60πcm² B、65πcm² C、120πcm² D、130πcm²

查看试题解析
9. 抛物线 $y = a x^{2} + b x + c$ 上部分点坐标如表所示，下列说法错误的是（）
x
…
－3
－2
－1
0
1
…
y
…
－6
0
4
6
6
…

A、抛物线与y轴的交点为(0，6) B、抛物线的对称轴是在y轴的右侧； C、抛物线一定经过点(3 ， 0) D、在对称轴左侧， y随x增大而减小．

查看试题解析
10.
如图，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，下述结论错误的是（　　）

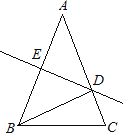A、BD平分∠ABC B、△BCD的周长等于AB＋BC C、AD=BD=BC D、点D是线段AC的中点

查看试题解析

二、填空题

11. 如果一组数a，2，4，0，5的中位数是4，那么a可以是（只需写出一个满足要求的数）．

查看试题解析
12. 有一个正六面体，六个面上分别写有1～6这6个整数，投掷这个正六面体一次，向上一面的数字是2的倍数或3的倍数的概率是．

查看试题解析
13. 如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为．

查看试题解析
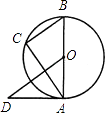14. 若|m|=4，|n|=3，且mn＜0，则m+n= ．

查看试题解析
15. 如图，已知点D是Rt△ABC的斜边BC上的一点，tanB= $\frac{1}{2}$ ，BC=3BD，CE⊥AD，则 $\frac{A E}{C E}$ = ．

查看试题解析
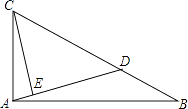16. 如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O₁ ， O₂ ， O₃ ， … 组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2016秒时，点P的坐标是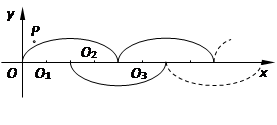

查看试题解析

三、综合题

17. 某区八年级有3000名学生参加“爱我中华知识竞赛”活动．为了了解本次知识竞赛的成绩分布情况，从中抽取了m名学生的得分进行统计
成绩x（分）
频数
频率
50≤x＜60
10
a
60≤x＜70
16
0.08
70≤x＜80
b
0.02
80≤x＜90
62
c
90≤x＜100
72
0.36
请你根据不完整的表格，回答下列问题：

(1)、请直接写出m，a，b，c的值；

(2)、若将得分转化为等级，规定50≤x＜60评为“D”，60≤x＜70评为“C”，70≤x＜90评为“B”，90≤x＜100评为“A”．这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”？

查看试题解析
18. 如图，直线y=﹣x+10与x轴、y轴分别交于点B，C，点A的坐标为（8，0），P（x，y）是直线y=﹣x+10在第一象限内一个动点．

(1)、求△OPA的面积S与x的函数关系式，并写出自变量的x的取值范围；

(2)、当△OPA的面积为10时，求点P的坐标．

查看试题解析
19. 如图，在 $Δ$ ABC中，点D在边BC上，联结AD，∠ADB=∠CDE，DE交边AC于点E，DE交BA延长线于点F，且 $A D^{2} = D E \cdot D F$ ．

(1)、求证： $Δ B F D$ ∽ $Δ C A D$ ；

(2)、求证： $B F \cdot D E = A B \cdot A D$ ．

查看试题解析
20. 某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体实验．测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当4≤x≤10时，y与x成反比例)．

(1)、根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式；

(2)、问血液中药物浓度不低于4微克/毫升的持续时间为多少小时？

查看试题解析
21. 如图，正方形ABCD中，E，F分别在AD，DC上，EF的延长线交BC的延长线于G点，且∠AEB=∠BEG；

(1)、求证：∠ABE= $\frac{1}{2}$ ∠BGE；

(2)、若AB=4，AE=1，求S_△_BEG ．

查看试题解析
22. 如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以 PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O．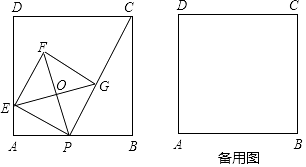

(1)、若AP=1，则AE=；

(2)、①求证：点O一定在△APE的外接圆上；
②当点P从点A运动到点B时，点O也随之运动，求点O经过的路径长；

(3)、在点P从点A到点B的运动过程中，△APE的外接圆的圆心也随之运动，求该圆心到AB边的距离的最大值．

查看试题解析
23.
如图，二次函数 $y = x^{2} + b x + c$ 的图像与 $x$ 轴交于 $Α$ 、 $Β$ 两点，与 $y$ 轴交于点 $C$ ， $Ο Β = Ο C$ ．点 $D$ 在函数图象上， $CD// x$ 轴，且 $CD = 2$ ，直线 $l$ 是抛物线的对称轴， $Ε$ 是抛物线的顶点．
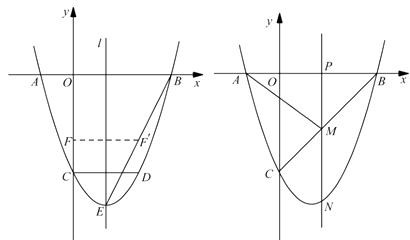
图 ① 图②

(1)、求 $b$ 、 $c$ 的值；

(2)、如图①，连接 $Β Ε$ ，线段 $Ο C$ 上的点 $F$ 关于直线 $l$ 的对称点 $F^{'}$ 恰好在线段 $Β Ε$ 上，求点 $F$ 的坐标；

(3)、如图②，动点 $Ρ$ 在线段 $Ο Β$ 上，过点 $Ρ$ 作 $x$ 轴的垂线分别与 $Β C$ 交于点 $Μ$ ，与抛物线交于点 $Ν$ ．试问：抛物线上是否存在点 $Q$ ，使得 $Δ Ρ Q Ν$ 与 $Δ Α Ρ Μ$ 的面积相等，且线段 $Ν Q$ 的长度最小？如果存在，求出点 $Q$ 的坐标；如果不存在，说明理由．

查看试题解析

成绩x（分）	频数	频率
50≤x＜60	10	a
60≤x＜70	16	0.08
70≤x＜80	b	0.02
80≤x＜90	62	c
90≤x＜100	72	0.36

x	…	－3	－2	－1	0	1	…
y	…	－6	0	4	6	6	…