2018年浙江省杭州市中考数学冲刺模拟卷(2)
试卷更新日期:2018-05-18 类型:中考模拟
一、单选题
-
1. 36的算术平方根是( )
A、±6 B、6 C、± D、2. 如图,l1∥l2∥l3 , 直线a,b与l1 , l2 , l3分别相交于点A、B、C和点D、E、F,
若 ,DE=4,则DF的长是( )
A、 B、 C、10 D、63. 在下面四个几何体中,俯视图是三角形的是( )
A、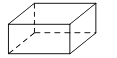 B、
B、 C、
C、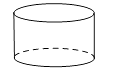 D、
D、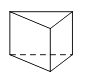 4. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( )
4. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( ) A、8,6 B、8,5 C、52,53 D、52,525. 如果一个三角形的三边长分别为1,k,3,则化简7−−|2k−3|的结果是( )A、-5 B、1 C、13 D、19-4k6. 一项工程甲单独做要40天完成,乙单独做需要50天完成,甲先单独做4天,然后两人合作x天完成这项工程,则可列的方程是( )A、 B、 C、 D、7. 如图,反比例函数y=的图象经过点A(2,1),若y≤1,则x的范围为( )
A、8,6 B、8,5 C、52,53 D、52,525. 如果一个三角形的三边长分别为1,k,3,则化简7−−|2k−3|的结果是( )A、-5 B、1 C、13 D、19-4k6. 一项工程甲单独做要40天完成,乙单独做需要50天完成,甲先单独做4天,然后两人合作x天完成这项工程,则可列的方程是( )A、 B、 C、 D、7. 如图,反比例函数y=的图象经过点A(2,1),若y≤1,则x的范围为( )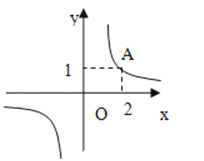 A、x≥1 B、x≥2 C、x<0或0<x≤1 D、x<0或x≥28. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A、x≥1 B、x≥2 C、x<0或0<x≤1 D、x<0或x≥28. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )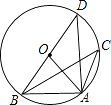 A、4 B、6 C、8 D、129. 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
A、4 B、6 C、8 D、129. 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )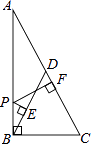 A、 B、 C、 D、10. 任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)= . 例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)== . 给出下列关于F(n)的说法:(1)F(2)=;(2)F(24)=;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、10. 任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)= . 例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)== . 给出下列关于F(n)的说法:(1)F(2)=;(2)F(24)=;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为 .
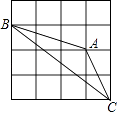 12. 某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,则表示“无所谓”的家长人数为 .
12. 某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,则表示“无所谓”的家长人数为 .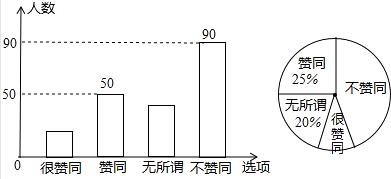 13. 分解因式:4a2﹣25b2= .14. 在直角坐标系中,O为坐标原点,已知点A(1,2),在y轴的正半轴上确定点P,使△AOP为等腰三角形,则点P的坐标为 .15. 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为 cm.
13. 分解因式:4a2﹣25b2= .14. 在直角坐标系中,O为坐标原点,已知点A(1,2),在y轴的正半轴上确定点P,使△AOP为等腰三角形,则点P的坐标为 .15. 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为 cm.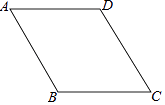 16. 若关于x的方程 =3的解为非负数,则m的取值范围是 .
16. 若关于x的方程 =3的解为非负数,则m的取值范围是 .三、解答题
-
17. 阅读下面的解题过程:
计算:(﹣ )÷( ﹣ + ﹣ )
方法一:原式=(﹣ )÷[( + )﹣( + )]=(﹣ )÷( ﹣ )=﹣ ×3=﹣
方法二:原式的倒数为( ﹣ + ﹣ )÷(﹣ )=( ﹣ + ﹣ )×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=﹣
通过阅读以上解题过程,你认为哪种方法更简单,选择合适的方法计算下题:
(﹣ )÷( ﹣ + ﹣ ).
18. 为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
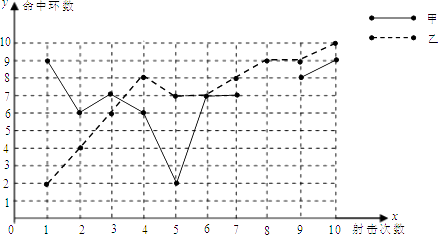 (1)、请补全上述图表(请直接在表中填空和补全折线图);(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)、如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?19. 如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.
(1)、请补全上述图表(请直接在表中填空和补全折线图);(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)、如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?19. 如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.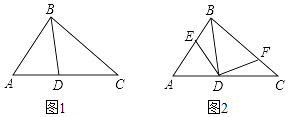 (1)、求证:∠ACB=∠ABD;(2)、现有点E、F分别在边AB、BC上如图2,满足∠EDF=∠A+∠C,当AB=4,BC=5,CA=6时,求证:DE=DF.20. 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)、求证:∠ACB=∠ABD;(2)、现有点E、F分别在边AB、BC上如图2,满足∠EDF=∠A+∠C,当AB=4,BC=5,CA=6时,求证:DE=DF.20. 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.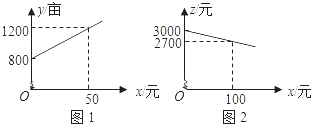 (1)、在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?(2)、分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;(3)、要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.21. 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)、在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?(2)、分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;(3)、要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.21. 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.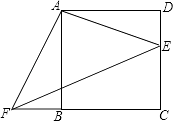 (1)、填空:△ABF可以由△ADE绕旋转中心点 , 按逆时针方向旋转度得到;(2)、若BC=8,DE=6,求△AEF的面积.22. 已知:如图,直线y=﹣ x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
(1)、填空:△ABF可以由△ADE绕旋转中心点 , 按逆时针方向旋转度得到;(2)、若BC=8,DE=6,求△AEF的面积.22. 已知:如图,直线y=﹣ x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0). (1)、求抛物线的解析式;(2)、点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大?若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;(3)、过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.23. 已知在矩形ABCD中,AB=2,AD=4. P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F. 联结AP,画∠FPE=∠BAP,PE交BF于点E.设PD=x,EF=y.
(1)、求抛物线的解析式;(2)、点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大?若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;(3)、过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.23. 已知在矩形ABCD中,AB=2,AD=4. P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F. 联结AP,画∠FPE=∠BAP,PE交BF于点E.设PD=x,EF=y.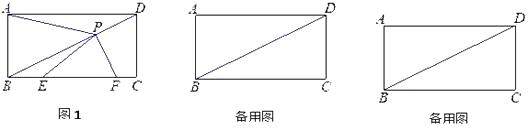 (1)、当点A、P、F在一条直线上时,求 ABF的面积;(2)、如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;(3)、联结PC,若∠FPC=∠BPE,请直接写出PD的长.
(1)、当点A、P、F在一条直线上时,求 ABF的面积;(2)、如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;(3)、联结PC,若∠FPC=∠BPE,请直接写出PD的长.