山西吕梁孝义2015-2016学年八年级下学期数学期末考试试卷
试卷更新日期:2018-05-17 类型:期末考试
一、单选题
-
1. 函数y= 中自变量x的取值范围是( )
A、x>5 B、x<5 C、x≠5 D、x=52. 下列计算正确的是( )A、3 - =3 B、 + = C、 D、23. 直角三角形中,两直角边分别是12和5,则斜边上的中线长是( ).A、34 B、26 C、6.5 D、8.54. 一组数据,3,4,6,5,6,则这组数据的众数、中位数分别是( )A、5,6 B、5,5 C、6,5 D、6,65. 已知一次函数y=ax+2的图象与x轴的交点坐标为(3,0),则一元二次方程ax+2=0的解为( )
A、x=3 B、x=0 C、x=2 D、x=a6. 小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )A、255分 B、84分 C、84.5分 D、86分7. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、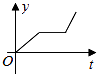 B、
B、 C、
C、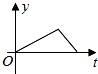 D、
D、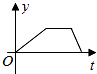 8. 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
8. 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )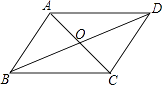 A、AO=OD B、AO⊥OD C、AO=OC D、AO⊥AB9. 如图,菱形ABCD的周长为8m,高AE的长为 cm,则对角线BD的长为( )
A、AO=OD B、AO⊥OD C、AO=OC D、AO⊥AB9. 如图,菱形ABCD的周长为8m,高AE的长为 cm,则对角线BD的长为( )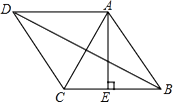 A、2cm B、3cm C、 cm D、2 cm10. 如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )A、8cm B、5 cm C、5.5cm D、1cm
A、2cm B、3cm C、 cm D、2 cm10. 如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )A、8cm B、5 cm C、5.5cm D、1cm二、填空题
-
11. 计算:3 -2 - = .12. 直线y=-3x+m经过点A(-1,a)、B(4,b),则ab(填“>”或“<”)13. 我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛,组织了选拔测试,分别对两人进行了五次测试,成绩(单位:秒)以及平均数、方差如表:
甲
13
13
14
16
18
=14.8
=3.76
乙
14
14
15
15
16
=14.8
=0.56
学校决定派乙运动员参加比赛,理由是 .
14. 一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有米.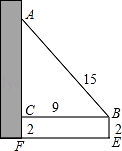 15. 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 .
15. 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 . 16. 如图,直线y=x+1与x轴交于点A,与y轴交于点B,正方形OCDE的顶点D在线段AB上,点C在y轴上,点E在x轴上,则点D的坐标为 .
16. 如图,直线y=x+1与x轴交于点A,与y轴交于点B,正方形OCDE的顶点D在线段AB上,点C在y轴上,点E在x轴上,则点D的坐标为 .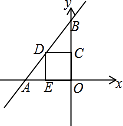
三、解答题
-
17. 计算:(1+ )2+3(1+ )(1- )18. 如图,在平面直角坐标系中,直线y=kx+b与x轴交于点A,与y轴交于点B,且四边形AOBC是矩形,BC=6,矩形AOBC的面积为18.
 (1)、求线段OC的长.(2)、求直线AB的解析式.19. 如图是三个正方形的网格,每个小正方形的边长是1,请你分别在三个网格图中画出面积为5的平行四边形、矩形、正方形.
(1)、求线段OC的长.(2)、求直线AB的解析式.19. 如图是三个正方形的网格,每个小正方形的边长是1,请你分别在三个网格图中画出面积为5的平行四边形、矩形、正方形.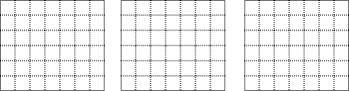
要求:①图形的顶点在格点上;②所画图形用阴影表示;③不写结论.
20. “节约用水、人人有责”,某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量比4月份有所下降,并且将5月份各户居民的节水量统计整理成如图所示的统计图表节水量/立方米
1
1.5
2.5
3
户数/户
50
80
a
70
 (1)、写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数.(2)、根据题意,将5月份各居民的节水量的条形统计图补充完整.(3)、求该小区300户居民5月份平均每户节约用水量,若用每立方米水需4元水费,请你估算每户居民1年可节约多少元钱的水费?
(1)、写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数.(2)、根据题意,将5月份各居民的节水量的条形统计图补充完整.(3)、求该小区300户居民5月份平均每户节约用水量,若用每立方米水需4元水费,请你估算每户居民1年可节约多少元钱的水费?
21. 数学活动课上,老师提出了一个问题:如图1,A、B两点被池塘隔开,在AB外选一点,连接AC和BC,怎样测出A、B两点的距离?

【活动探究】学生以小组展开讨论,总结出以下方法:
⑴如图2,选取点C,使AC=BC=a,∠C=60°;
⑵如图3,选取点C,使AC=BC=b,∠C=90°;
⑶如图4,选取点C,连接AC,BC,然后取AC、BC的中点D、E,量得DE=c…
【活动总结】
(1)、请根据上述三种方法,依次写出A、B两点的距离.(用含字母的代数式表示)并写出方法⑶所根据的定理.AB= , AB= , AB= .
定理: .
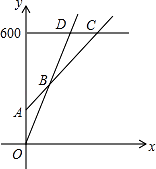
(2)、请你再设计一种测量方法,(图5)画出图形,简要说明过程及结果即可.22. 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元
 (1)、分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(1)、分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)、在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)、请根据函数图象,直接写出选择哪种消费方式更合算.23.(1)、如图①,在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF分别交AD、BC于点E、F,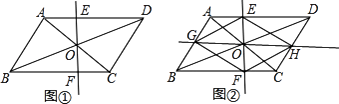
求证:OE=OF.
(2)、在图①中,过点O作直线GH分别交AB、CD于点G、H,且满足GH⊥EF,连结EG、GF、FH、HE.如图②,试判断四边形EGFH的形状,并说明理由;(3)、在(2)的条件下,若平行四边形ABCD变为矩形时,四边形EGFH是;
若平行四边形ABCD变为菱形时,四边形EGFH是;
若平行四边形ABCD变为正方形时,四边形EGFH是 .