山西临汾洪洞县2015-2016学年八年级下学期数学期末考试试卷
试卷更新日期:2018-05-17 类型:期末考试
一、单选题
-
1. 下列各式 (1-x), , , +x, ,其中分式共有( )个.A、2 B、3 C、4 D、52. 函数y= 中,自变量x的取值范围是( )A、x>2 B、x≠2 C、x>-1 D、x≠-13. 二十一世纪,纳米技术将被广泛应用,纳米是长度计量单位,1纳米=0.000000001米,则5纳米可以用科学记数法表示为( )
A、5×109米 B、50×10-8米 C、5×10-9米 D、5×10-8米4. 下列命题是假命题的是( )A、菱形的对角线互相垂直平分 B、有一斜边与一直角边对应相等的两直角三角形全等 C、有一组邻边相等且垂直的平行四边形是正方形 D、对角线相等的四边形是矩形5. 对于数据:80,88,85,85,83,83,84.下列说法中错误的有( )A、这组数据的平均数是84;
B、这组数据的众数是85;
C、这组数据的中位数是84;
D、这组数据的方差是36.
A、1个 B、2个 C、3个 D、4个6. 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )A、 B、 C、 D、7. 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )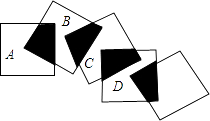 A、2cm2 B、4cm2 C、6cm2 D、8cm28. “已知:正比例函数y1=kx(k>0)与反比例函数y2= (m>0)图象相交于A、B两点,其横坐标分别是1和-1,求不等式kx> 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或-1<x<0时,y1>y2 , 所以不等式kx> 的解集是x>1或-1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
A、2cm2 B、4cm2 C、6cm2 D、8cm28. “已知:正比例函数y1=kx(k>0)与反比例函数y2= (m>0)图象相交于A、B两点,其横坐标分别是1和-1,求不等式kx> 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或-1<x<0时,y1>y2 , 所以不等式kx> 的解集是x>1或-1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
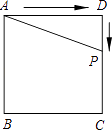
A、数形结合 B、转化 C、类比 D、分类讨论9. 已知四边形ABCD,下列说法正确的是( )A、当AD=BC,AB∥DC时,四边形ABCD是平行四边形 B、当AD=BC,AB=DC时,四边形ABCD是平行四边形 C、当AC=BD,AC平分BD时,四边形ABCD是矩形 D、当AC=BD,AC⊥BD时,四边形ABCD是正方形10.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
 A、
A、 B、
B、 C、
C、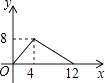 D、
D、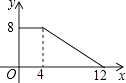
二、填空题
-
11. 若分式 的值为零,则x= .12. 在y=5x+a-2中,若y是x的正比例函数,则常数a= .13. 在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差为1.2,乙的成绩的方差为3.9,由此可知的成绩更稳定.14. 定义运算“★”:对于任意实数a,b,都有a★b=a2+b,如:2★4=22+4=8.若(x-1)★3=7,则实数x的值是 .
15. 如图,在矩形ABCD中,DE⊥AC,∠ADE= ∠CDE,那么∠BDC的度数为 . 16. 如图,已知:在▱ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点,则EF+BF的最小值为 .
16. 如图,已知:在▱ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点,则EF+BF的最小值为 .
三、解答题
-
17. 先化简,再求值: • ,其中x=2+ ,y=2- .18. 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元
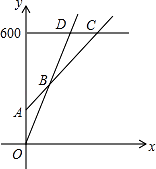 (1)、分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(1)、分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)、在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)、请根据函数图象,直接写出选择哪种消费方式更合算.19. 平行四边形的2个顶点的坐标为(-3,0),(1,0),第三个顶点在y轴上,且与x轴的距离是3个单位,求第四个顶点的坐标.20. 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.求证:四边形AECF是矩形.
 21. 房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:
21. 房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题: (1)、这次抽样调查中,共调查了名学生;(2)、补全两幅统计图;(3)、根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
(1)、这次抽样调查中,共调查了名学生;(2)、补全两幅统计图;(3)、根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?