上海市奉贤区2018届数学中考一模试卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列函数中是二次函数的是（）

A、y=2（x﹣1） B、y=（x﹣1）²﹣x² C、y=a（x﹣1）² D、y=2x²﹣1

查看试题解析
2. 在Rt△ABC中，∠C=90°，如果AC=2，cosA= $\frac{2}{3}$ ，那么AB的长是（）

A、3 B、 $\frac{4}{3}$ C、 $\sqrt{5}$ D、 $\sqrt{13}$

查看试题解析
3. 在△ABC中，点D，E分别在AB，AC上，如果AD：BD=1：3，那么下列条件中能够判断DE∥BC的是（）

A、 $\frac{D E}{B C} = \frac{1}{4}$ B、 $\frac{A D}{A B} = \frac{1}{4}$ C、 $\frac{A E}{A C} = \frac{1}{4}$ D、 $\frac{A E}{E C} = \frac{1}{4}$

查看试题解析
4. 设n为正整数， $\vec{a}$ 为非零向量，那么下列说法不正确的是（）

A、n $\vec{a}$ 表示n个 $\vec{a}$ 相乘 B、-n $\vec{a}$ 表示n个- $\vec{a}$ 相加 C、n $\vec{a}$ 与 $\vec{a}$ 是平行向量 D、-n $\vec{a}$ 与n $\vec{a}$ 互为相反向量

查看试题解析
5. 如图，电线杆CD的高度为h，两根拉线AC与BC互相垂直（A，D，B在同一条直线上），设∠CAB=α，那么拉线BC的长度为（）

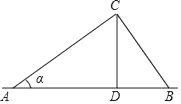A、 $\frac{h}{sin α}$ B、 $\frac{h}{cos α}$ C、 $\frac{h}{tan α}$ D、 $\frac{h}{cot α}$

查看试题解析
6. 已知二次函数y=ax²+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表：
x … -1 0 1 2 …
y … 0 3 4 3 …
那么关于它的图象，下列判断正确的是（）

A、开口向上 B、与x轴的另一个交点是（3，0） C、与y轴交于负半轴 D、在直线x=1的左侧部分是下降的

查看试题解析

二、填空题

7. 已知5a=4b，那么 $\frac{a + b}{b}$ = ．

查看试题解析
8. 计算：tan60°﹣cos30°= ．

查看试题解析
9. 如果抛物线y=ax²+5的顶点是它的最低点，那么a的取值范围是．

查看试题解析
10. 如果抛物线y=2x²与抛物线y=ax²关于x轴对称，那么a的值是．

查看试题解析
11. 如果向量 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{x}$ 满足关系式4 $\vec{a}$ ﹣（ $\vec{b}$ ﹣ $\vec{x}$ ）= $\vec{0}$ ，那么 $\vec{x}$ = ．（用向量 $\vec{a}$ 、 $\vec{b}$ 表示）

查看试题解析
12. 某快递公司十月份快递件数是10万件，如果该公司第四季度每个月快递件数的增长率都为x（x＞0），十二月份的快递件数为y万件，那么y关于x的函数解析式是．

查看试题解析
13. 如图，l₁∥l₂∥l₃ ，两条直线与这三条平行线分别交于点A、B、C和D、E、F，已知 $\frac{A B}{B C} = \frac{3}{2}$ ，则 $\frac{D E}{D F}$ 的值为．

查看试题解析
14. 如果两个相似三角形的面积的比是4：9，那么它们对应的角平分线的比是．

查看试题解析
15. 如图，已知梯形ABCD中，AB∥CD，对角线AC、BD相交于点O，如果S_△_AOB=2S_△_AOD ， AB=10，那么CD的长是．

查看试题解析
16. 已知AD、BE是△ABC的中线，AD、BE相交于点F，如果AD=6，那么AF的长是．

查看试题解析
17. 如图，在△ABC中，AB=AC，AH⊥BC，垂足为点H，如果AH=BC，那么sin∠BAC的值是．

查看试题解析
18. 已知△ABC，AB=AC，BC=8，点D、E分别在边BC、AB上，将△ABC沿着直线DE翻折，点B落在边AC上的点M处，且AC=4AM，设BD=m，那么∠ACB的正切值是．（用含m的代数式表示）

查看试题解析

三、解答题

19. 已知抛物线y=﹣2x²﹣4x+1．

(1)、求这个抛物线的对称轴和顶点坐标；

(2)、将这个抛物线平移，使顶点移到点P（2，0）的位置，写出所得新抛物线的表达式和平移的过程．

查看试题解析
20. 已知：如图，在平行四边形ABCD中，AD=2，点E是边BC的中点，AE、BD相交于点F，过点F作FG∥BC，交边DC于点G．

(1)、求FG的长；

(2)、设 $\overset{⇀}{A D} = \overset{⇀}{a}$ ， $\overset{⇀}{D C} = \overset{⇀}{b}$ ，用 $\overset{⇀}{a}$ 、 $\overset{⇀}{b}$ 的线性组合表示 $\overset{⇀}{A F}$ ．

查看试题解析
21. 已知：如图，在Rt△ABC中，∠ACB=90°，BC= $\sqrt{3}$ ，cot∠ABC= $\frac{\sqrt{2}}{2}$ ，点D是AC的中点．

(1)、求线段BD的长；

(2)、点E在边AB上，且CE=CB，求△ACE的面积．

查看试题解析
22. 如图，为了将货物装入大型的集装箱卡车，需要利用传送带AB将货物从地面传送到高1.8米（即BD=1.8米）的操作平台BC上．已知传送带AB与地面所成斜坡的坡角∠BAD=37°．

(1)、求传送带AB的长度；

(2)、因实际需要，现在操作平台和传送带进行改造，如图中虚线所示，操作平台加高0.2米（即BF=0.2米），传送带与地面所成斜坡的坡度i=1：2．求改造后传送带EF的长度．（精确到0.1米）（参考数值：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{2}$ ≈1.41， $\sqrt{5}$ ≈2.24）

查看试题解析
23. 已知：如图，四边形ABCD，∠DCB=90°，对角线BD⊥AD，点E是边AB的中点，CE与BD相交于点F，BD²=AB•BC

(1)、求证：BD平分∠ABC；

(2)、求证：BE•CF=BC•EF．

查看试题解析
24. 如图，在平面直角坐标系xOy中，已知抛物线y= $\frac{3}{8} x^{2} + b x + c$ 与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，﹣3），经过点A的射线AM与y轴相交于点E，与抛物线的另一个交点为F，且 $\frac{A E}{E F} = \frac{1}{3}$ .

(1)、求这条抛物线的表达式，并写出它的对称轴；

(2)、求∠FAB的余切值；

(3)、点D是点C关于抛物线对称轴的对称点，点P是y轴上一点，且∠AFP=∠DAB，求点P的坐标．

查看试题解析
25. 已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．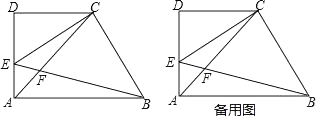

(1)、用含x的代数式表示线段CF的长；

(2)、如果把△CAE的周长记作C_△_CAE ， △BAF的周长记作C_△_BAF ，设 $\frac{C_{Δ C A E}}{C_{Δ B A F}}$ =y，求y关于x的函数关系式，并写出它的定义域；

(3)、当∠ABE的正切值是 $\frac{3}{5}$ 时，求AB的长．

查看试题解析

x	…	-1	0	1	2	…
y	…	0	3	4	3	…