山西省2018届数学中考信息冲刺卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，在数轴上，点A表示的数的绝对值是（）

A、2 B、－ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、－2

查看试题解析
2. 下列WORD软件自选图形中，是轴对称图形而不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

甲
乙
丙
丁
平均数(cm)
180
180
185
185
方差
2.1
3.6
7.4
2.1
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 已知a²－6a－m是一个完全平方式，则常数m等于（）

A、9 B、－9 C、12 D、－12

查看试题解析
5. 据2018年2月9日，山西省统计局《2017年山西省人口变动情况抽样调查主要数据公报》显示，根据抽样调查推算，太原市2017年底常住人口约4 380 000人，在全省11个地市中排名第三. 4 380 000用科学记数法可表示为（）

A、438×10⁴ B、4.38×10⁵ C、4.38×10⁶ D、0.438×10⁷

查看试题解析
6. 如图是由6个大小相同的正方体组成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
7. 方程 $\frac{1}{x - 1} - \frac{2}{x + 3}$ ＝0的解为（）

A、x＝3 B、x＝4 C、x＝5 D、x＝－5

查看试题解析
8. 在反比例函数 $y = \frac{k - 1}{x}$ 的图象的每一个分支上，y都随x的增大而减小，则k的取值范围是（）

A、k＞1 B、k＞0 C、k≥1 D、k＜1

查看试题解析
9. 如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．则∠ABD的度数是（）

A、30° B、25° C、20° D、15°

查看试题解析
10. 如图，将一张圆形纸片对折三次后，沿图④中的虚线AB剪下(点A和点B均为半径的中点)，得到两部分，去掉有圆弧的部分，剩余部分展开后得到的正多边形的每个内角是（）

A、90° B、120° C、135° D、150°

查看试题解析

二、填空题

11. 计算：3a²·a⁴－(－2a³)²＝．

查看试题解析
12. 在学校组织的“爱我中华，歌唱祖国”歌咏比赛中，共有18名同学参加决赛，他们的成绩如下表：
成绩(分)
9.40
9.50
9.60
9.70
9.80
9.90
人数
2
3
5
4
3
1
这些同学决赛成绩的中位数是．

查看试题解析
13. 将一些形状相同的“ ”按下图所示的规律摆放，则第n个图形中有个“ ”．

查看试题解析
14. 黄金分割具有严格的比例性，蕴藏着丰富的美学价值，这一比值能够引起人们的美感．如图，连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形，我们把这种三角形称为“黄金三角形”，黄金三角形的底与腰之比为 $\frac{\sqrt{5} - 1}{2}$ .若MN＝ $\sqrt{5}$ －1，则AB＝．

查看试题解析
15. 如图，已知线段AB⊥CD，E，F分别是AD，CB的中点，且AB＝16，CD＝12，则EF的长是.

查看试题解析

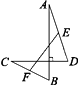
三、解答题

16. 计算

(1)、计算：－ ${(\frac{1}{2})}^{- 1}$ ＋| $\sqrt{3}$ －2|＋ $\sqrt{12}$ ＋4cos30°；

(2)、化简：(a＋1)÷ $(\frac{1 + a^{2}}{a} + 2)$ ＋ $\frac{1 - a}{a + 1}$ .

查看试题解析
17. 下面方格中有一个四边形ABCD和点O，请在方格中画出以下图形(只要求画出平移、旋转后的图形，不要求写出作图步骤和过程)．

(1)、①画出四边形ABCD以点O为旋转中心，逆时针旋转90°后得到的四边形A₁B₁C₁D₁；
②画出四边形A₁B₁C₁D₁向右平移3格(3个小方格的边长)后得到的四边形A₂B₂C₂D₂；

(2)、填空：若每个小方格的边长为1，则四边形A₁B₁C₁D₁与四边形A₂B₂C₂D₂重叠部分的面积为．

查看试题解析
18. 阅读思考：
数学课上老师出了一道分式化简求值题目．
题目： $\frac{x^{2} + x}{x - 1}$ ÷(x＋1)· $\frac{1}{x + 1}$ － $\frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，其中x＝－ $\frac{1}{2}$ .
“勤奋”小组的杨明同学展示了他的解法：
解：原式＝ $\frac{x^{2} + x}{x - 1}$ － $\frac{x^{2} - x}{x^{2} - 2 x + 1}$ ..................第一步
＝ $\frac{x^{2} + x}{x - 1}$ － $\frac{x (x - 1)}{{(x - 1)}^{2}}$ ................ ..第二步
＝ $\frac{x^{2} + x - x}{x - 1}$ ..........................第三步
＝ $\frac{x^{2}}{x - 1}$ ..................................第四步
当x＝－ $\frac{1}{2}$ 时，原式＝ $\frac{{(\frac{1}{2})}^{2}}{- \frac{1}{2} - 1} = - \frac{1}{6}$ .......................第五步
请你认真阅读上述解题过程，并回答问题：
你认为该同学的解法正确吗？如有错误，请指出错误在第几步，并写出完整、正确的解答过程．

查看试题解析
19. 图1所示是一枚质地均匀的骰子．骰子有六个面并分别代表数字1，2，3，4，5，6.如图2，正六边形ABCDEF的顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子向上的一面上的点数是几，就沿正六边形的边顺时针方向连续跳几个边长．如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D；若第二次掷得2，就从圈D开始顺时针连续跳2个边长，落到圈F……
设游戏者从圈A起跳．

(1)、小明随机掷一次骰子，求落回到圈A的概率P₁；

(2)、小亮随机掷两次骰子，用列表法或画树状图法求最后落回到圈A的概率P₂ ，并指出他与小明落回到圈A的可能性一样吗？

查看试题解析
20. 永祚寺双塔，又名凌霄双塔，是山西省会太原现存古建筑中最高的建筑，位于太原市城区东南向山脚畔．数学活动小组的同学对其中一个塔进行了测量．测量方法如下：如图所示，间接测得该塔底部点B到地面上一点E的距离为48 m，塔的顶端为点A，且AB⊥CB，在点E处竖直放一根标杆，其顶端为D，在BE的延长线上找一点C，使C，D，A三点在同一直线上，测得CE＝2 m.

(1)、方法1，已知标杆DE＝2.2 m，求该塔的高度；

(2)、方法2，测量得∠ACB＝47.5°，已知tan47.5°≈1.09，求该塔的高度；

(3)、假如该塔的高度在方法1和方法2测得的结果之间，你认为该塔的高度大约是多少米？

查看试题解析
21. 某网店以每个24元的价格购进了600个水杯，第一个月以每个36元销售，售出了200个；第二个月该网店为了增加销量，决定在第一个月价格的基础上降价销售，根据市场调查，单价每降低1元，可多售出20个，但最低售价应高于购进的价格；第二个月结束后，该网店计划将剩余的水杯捐赠某山区，捐赠所需邮寄费共40元，设第二个月单价降低了x元．

(1)、填表：(列式不需要化简)
时间
第一个月
第二个月
单价(元)
36
总销量(个)
200

(2)、如果该网店希望通过销售这批水杯获利2 360元，那么第二个月每个水杯的售价应是多少元？

查看试题解析
22. 数学活动
问题情境：
如图1，在∆ABC中，AB＝AC，∠BAC＝90°，D，E分别是边AB，AC的中点，将∆ADE绕点A顺时针旋转α角(0°＜α＜90°)得到∆AD′E′，连接CE′，BD′.探究CE′与BD′的数量关系；
探究发现：

(1)、图1中，CE′与BD′的数量关系是；

(2)、如图2，若将问题中的条件“D，E分别是边AB，AC的中点”改为“D为AB边上任意一点，DE∥BC交AC于点E”，其他条件不变，(1)中CE′与BD′的数量关系还成立吗？请说明理由；

(3)、如图3，在(2)的条件下，连接BE′，CD′，分别取BC，CD′，E′D′，BE′的中点F，G，H，I，顺次连接F，G，H，I得到四边形FGHI.请判断四边形FGHI的形状，并说明理由；

(4)、如图4，在∆ABC中，AB＝AC，∠BAC＝60°，点D，E分别在AB，AC上，且DE∥BC，将∆ADE绕点A顺时针旋转60°得到∆AD′E′，连接CE′，BD′.请你仔细观察，提出一个你最关心的数学问题(例如：CE′与BD′相等吗？)．

查看试题解析
23. 如图，二次函数y＝x²－4x＋3的图象与x轴交于A，B两点(点B在点A的右侧)，与y轴交于点C，抛物线的对称轴与x轴交于点D.、
(备用图)

(1)、求点A，点B和点D的坐标；

(2)、在y轴上是否存在一点P，使∆PBC为等腰三角形？若存在，请求出点P的坐标；

(3)、若动点M从点A出发，以每秒1个单位长度的速度沿AB向点B运动，同时另一个动点N从点D出发，以每秒2个单位长度的速度在抛物线的对称轴上运动，当点M到达点B时，点M，N同时停止运动，问点M，N运动到何处时，∆MNB的面积最大，试求出最大面积．

查看试题解析

时间	第一个月	第二个月
单价(元)	36
总销量(个)	200

	甲	乙	丙	丁
平均数(cm)	180	180	185	185
方差	2.1	3.6	7.4	2.1

成绩(分)	9.40	9.50	9.60	9.70	9.80	9.90
人数	2	3	5	4	3	1