山东省滨州市2018届数学初中学业水平考试试卷
试卷更新日期:2018-05-17 类型:中考模拟
一、单选题
-
1. 在 , ,0,-2这四个数中,是无理数的为( )A、0 B、 C、 D、-22. 如果□×(-3)=1,则“□”内应填的实数是( )A、 B、3 C、-3 D、3. 如图,小手盖住的点的坐标可能为( )
 A、(-4,-5) B、(-4,5) C、(4,5) D、(4,-5)4. 已知实数a,b,若a>b,则下列结论错误的是( )A、a-7>b-7 B、6+a>b+6 C、 D、-3a>-3b5. 如图,直线l1∥l2 , 且分别与△ABC的两边AB、AC相交,若∠A=45°,∠1=65°,则∠2的度数为 ( )
A、(-4,-5) B、(-4,5) C、(4,5) D、(4,-5)4. 已知实数a,b,若a>b,则下列结论错误的是( )A、a-7>b-7 B、6+a>b+6 C、 D、-3a>-3b5. 如图,直线l1∥l2 , 且分别与△ABC的两边AB、AC相交,若∠A=45°,∠1=65°,则∠2的度数为 ( ) A、45° B、65° C、70° D、110°6. 如图,在点 中,一次函数 的图象不可能经过的点是( )
A、45° B、65° C、70° D、110°6. 如图,在点 中,一次函数 的图象不可能经过的点是( )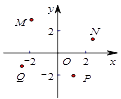 A、 B、 C、 D、7. 关于x的分式方程 的解为正实数,则实数m的取值范围是( )A、m<-6且m≠2 B、m>6且m≠2 C、m<6且m≠-2 D、m<6且m≠28. 将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,如图,则 的大小为( )
A、 B、 C、 D、7. 关于x的分式方程 的解为正实数,则实数m的取值范围是( )A、m<-6且m≠2 B、m>6且m≠2 C、m<6且m≠-2 D、m<6且m≠28. 将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,如图,则 的大小为( ) A、80° B、100° C、120° D、不能确定9. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )
A、80° B、100° C、120° D、不能确定9. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )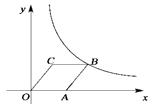 A、12 B、20 C、24 D、3210. 如图,有以下3个条件:①AC=AB;②AB∥CD;③∠1=∠2.从这三个条件中任选2个作为条件,另1个作为结论,则结论正确的概率是( )
A、12 B、20 C、24 D、3210. 如图,有以下3个条件:①AC=AB;②AB∥CD;③∠1=∠2.从这三个条件中任选2个作为条件,另1个作为结论,则结论正确的概率是( ) A、0 B、 C、 D、111. 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片 ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB, AC于点E,G.连接GF.则下列结论错误的是( )
A、0 B、 C、 D、111. 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片 ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB, AC于点E,G.连接GF.则下列结论错误的是( )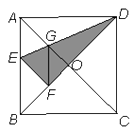 A、∠AGD=112.5° B、四边形AEFG是菱形 C、tan∠AED=2 D、BE=2OG12. 如图,点E为菱形ABCD边上的一个动点,并沿 的路径移动,设点E经过的路径长为x,△ADE的面积为y,则下列图象能大致反映y与x的函数关系的是( )
A、∠AGD=112.5° B、四边形AEFG是菱形 C、tan∠AED=2 D、BE=2OG12. 如图,点E为菱形ABCD边上的一个动点,并沿 的路径移动,设点E经过的路径长为x,△ADE的面积为y,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、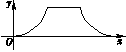 C、
C、 D、
D、
二、填空题
-
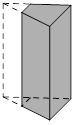
13. 计算: =.14. 不等式组 的解集为.15. 有一组数据:3,a,4,6,7,它们的平均数是5,则a= , 这组数据的方差是 .16. 经过两次连续降价,某药品销售单价由原来的49元降到30元,设该药品平均每次降价的百分率为x,根据题意可列方程是 .17. 如图,正三棱柱的底面周长为15,截去一个底面周长为6的正三棱柱,所得几何体的俯视图的周长是 , 面积是 .
 18. 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是海里.
18. 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是海里.
19. 如图,在平面直角坐标系中,点A的坐标为(﹣2, ),以原点O为中心,将点A顺时针旋转165°得到点A′,则点A′的坐标为. 20. 规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是 .
20. 规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是 .
三、解答题
-
21. 先化简后求值: ,其中x= .22. 已知:如图,在△ABC的中,AD是角平分线,E是AD上一点,且AB:AC=AE:AD.
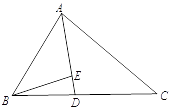
求证:
(1)、BE=BD;(2)、23. 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.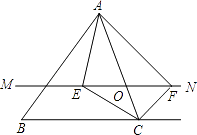 (1)、求证:EO=FO;(2)、当点O运动到何处时,四边形AECF是矩形?并证明你的结论.24. 已知:关于x的一元二次方程x2﹣(2m+3)x+m2+3m+2=0.(1)、已知x=2是方程的一个根,求m的值;(2)、以这个方程的两个实数根作为△ABC中AB、AC(AB<AC)的边长,当BC= 时,△ABC是等腰三角形,求此时m的值.25. 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,
(1)、求证:EO=FO;(2)、当点O运动到何处时,四边形AECF是矩形?并证明你的结论.24. 已知:关于x的一元二次方程x2﹣(2m+3)x+m2+3m+2=0.(1)、已知x=2是方程的一个根,求m的值;(2)、以这个方程的两个实数根作为△ABC中AB、AC(AB<AC)的边长,当BC= 时,△ABC是等腰三角形,求此时m的值.25. 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D, (1)、若PD∥BC,求证:AP平分∠CAB;(2)、若PB=BD,求PD的长度;(3)、证明:无论点P在 上的位置如何变化,CP•CQ为定值.26. 在平面直角坐标系中,已知点B的坐标是(-1,0),点A的坐标是(4,0),点C的坐标是(0,4),抛物线过A,B,C三点.
(1)、若PD∥BC,求证:AP平分∠CAB;(2)、若PB=BD,求PD的长度;(3)、证明:无论点P在 上的位置如何变化,CP•CQ为定值.26. 在平面直角坐标系中,已知点B的坐标是(-1,0),点A的坐标是(4,0),点C的坐标是(0,4),抛物线过A,B,C三点. (1)、求抛物线的解析式;(2)、点 是抛物线上的一点(点 在直线 上方),过点 作 轴,垂足为 ,交 于点 ,当线段 与 互相平分时,求出点 的坐标;(3)、抛物线的对称轴为l,顶点为K,点C关于l对称点为J.是否存在 x轴上的点Q、y轴上的点R,使四边形KJQR的周长最小?若存在,写出探寻满足条件的点的过程并画图;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点 是抛物线上的一点(点 在直线 上方),过点 作 轴,垂足为 ,交 于点 ,当线段 与 互相平分时,求出点 的坐标;(3)、抛物线的对称轴为l,顶点为K,点C关于l对称点为J.是否存在 x轴上的点Q、y轴上的点R,使四边形KJQR的周长最小?若存在,写出探寻满足条件的点的过程并画图;若不存在,请说明理由.