江苏省无锡市丁蜀学区2018届九年级数学中考一模试卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣5的倒数是（）

A、 $\frac{1}{5}$ B、±5 C、5 D、﹣ $\frac{1}{5}$

查看试题解析
2. 函数y＝ $\frac{x}{2 - x}$ 中自变量x的取值范围是（）

A、x≠2 B、x≥2 C、x≤2 D、x＞2

查看试题解析
3. 分式 $\frac{2}{2 - x}$ 可变形为（）

A、 $\frac{2}{2 + x}$ B、 $- \frac{2}{2 + x}$ C、 $\frac{2}{x - 2}$ D、 $- \frac{2}{x - 2}$

查看试题解析
4. 已知A样本的数据如下：72，73，76，76，77，78，78，78，B样本的数据恰好是A样本数据每个都加2，则A，B两个样本的下列统计量对应相同的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
5. 若点A(3，－4)、B(－2，m)在同一个反比例函数的图象上，则m的值为（）

A、6 B、－6 C、12 D、－12

查看试题解析
6. 如图，AB∥CD，则根据图中标注的角，下列关系中成立的是（）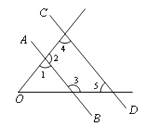

A、∠1＝∠3 B、∠2＋∠3＝180° C、∠2＋∠4＜180° D、∠3＋∠5＝180°

查看试题解析
7. 如图，A，B，C是⊙O上的三点，且∠ABC=70°，则∠AOC的度数是（）

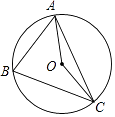A、35° B、140° C、70° D、70°或140°

查看试题解析
8. 如图，梯形ABCD中，AD∥BC，对角线AC、BD相交于O，AD=1，BC=4，则△AOD与△BOC的面积比等于（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{8}$ D、 $\frac{1}{16}$

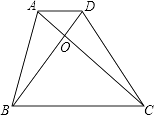查看试题解析
9. 如图，平行四边形ABCD中，AB∶BC=3∶2，∠DAB=60°，E在AB上，且AE∶EB=1∶2，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP∶DQ等于（）

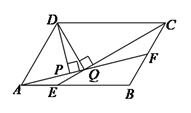A、3∶4 B、 $\sqrt{13}$ ∶ $2 \sqrt{5}$ C、 $\sqrt{13}$ ∶ $2 \sqrt{6}$ D、 $2 \sqrt{3}$ ∶ $\sqrt{13}$

查看试题解析

二、填空题

10. 分解因式：2x²－4x=.

查看试题解析
11. 去年，中央财政安排资金8 200 000 000元，免除城市义务教育学生学杂费，支持进城务工人员随迁子女公平接受义务教育，这个数据用科学记数法可表示为元.

查看试题解析
12. 一次函数y＝2x－6的图像与x轴的交点坐标为．

查看试题解析
13. 命题“全等三角形的面积相等”的逆命题是命题.(填“真”或“假”)

查看试题解析
14. 如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于．

查看试题解析
15. 如图，▱ABCD中，AE⊥BD于E，∠EAC＝30°，AE＝3，则AC的长等于．

查看试题解析
16. 如图，已知▱OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为．

查看试题解析
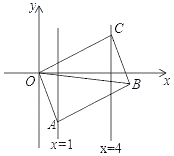17. 在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D都在格点处，AB与CD相交于O，则tan∠BOD的值等于．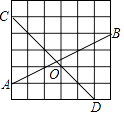

查看试题解析

三、解答题

18. 计算：

(1)、 $\sqrt{9} - {(- 2)}^{2} + {(- 0.1)}^{0}$ ；

(2)、(x+1)²－(x+2)(x－2)．

查看试题解析
19. 解答题

(1)、解方程： $\frac{5}{2 x - 1} = \frac{3}{x + 2}$ ．

(2)、解不等式组： ${\begin{matrix} 2 x + 3 > 1 ① \\ x - 2 \leq \frac{1}{2} (x + 2) ② \end{matrix}$

查看试题解析
20. 如图，已知：△ABC中，AB=AC，M是BC的中点，D、E分别是AB、AC边上的点，且BD=CE．求证：MD=ME．

查看试题解析
21. 某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查，其中有这样一个问题：老师在课堂上放手让学生提问和表达，
A从不 B很少 C有时 D常常 E总是
答题的学生在这五个选项中只能选择一项．下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图．
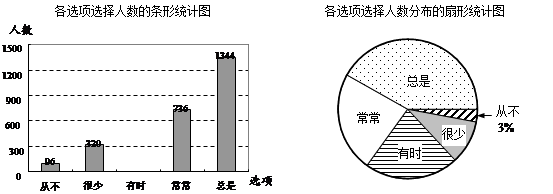
根据以上信息，解答下列问题：

(1)、该区共有名初二年级的学生参加了本次问卷调查；

(2)、请把这幅条形统计图补充完整；

(3)、在扇形统计图中，“总是”的圆心角为．（精确到度）

查看试题解析
22. 综合题

(1)、甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人．求第二次传球后球回到甲手里的概率．（请用“画树状图”的方式给出分析过程）

(2)、如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是（请直接写出结果）．

查看试题解析
23. 如图，OA=2，以点A为圆心，1为半径画⊙A与OA的延长线交于点C，过点A画OA的垂线，垂线与⊙A的一个交点为B，连接BC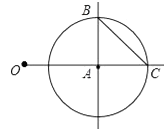

(1)、线段BC的长等于；

(2)、请在图中按下列要求逐一操作，并回答问题：
①以点为圆心，以线段的长为半径画弧，与射线BA交于点D，使线段OD的长等于 $\sqrt{6}$ ；
②连OD，在OD上画出点P，使OP的长等于 $\frac{2 \sqrt{6}}{3}$ ，请写出画法，并说明理由．

查看试题解析
24. 某校计划购买一批篮球和足球，已知购买2个篮球和1个足球共需320元，购买3个篮球和2个足球共需540元．

(1)、求每个篮球和每个足球的售价；

(2)、如果学校计划购买这两种球共50个，总费用不超过5500元，那么最多可购买多少个足球？

查看试题解析
25. 如图，直线x=﹣4与x轴交于点E，一开口向上的抛物线过原点交线段OE于点A，交直线x=﹣4于点B，过B且平行于x轴的直线与抛物线交于点C，直线OC交直线AB于D，且AD：BD=1：3．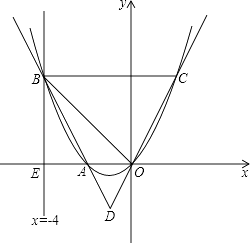

(1)、求点A的坐标；

(2)、若△OBC是等腰三角形，求此抛物线的函数关系式．

查看试题解析
26. 如图1，菱形ABCD中，∠A=60°，点P从A出发，以2cm/s的速度沿边AB、BC、CD匀速运动到D终止，点Q从A与P同时出发，沿边AD匀速运动到D终止，设点P运动的时间为t（s）．△APQ的面积S（cm²）与t（s）之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出．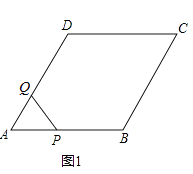

(1)、求点Q运动的速度；

(2)、求图2中线段FG的函数关系式；

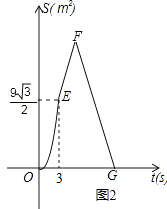(3)、问：是否存在这样的t，使PQ将菱形ABCD的面积恰好分成1：5的两部分？若存在，求出这样的t的值；若不存在，请说明理由．

查看试题解析
27. 如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．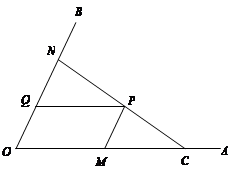

(1)、若∠AOB＝60º，OM＝4，OQ＝1，求证：CN⊥OB．

(2)、当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问： $\frac{1}{O M} - \frac{1}{O N}$ 的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
②设菱形OMPQ的面积为S₁ ， △NOC的面积为S₂ ，求 $\frac{S_{1}}{S_{2}}$ 的取值范围．

查看试题解析