河南省周口市西华县2018届数学中考一模试卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. －3是3的（）

A、倒数 B、相反数 C、绝对值 D、平方根

查看试题解析
2. “厉行勤俭节约，反对铺张浪费”势在必行，最新统计数据显示，中国每年浪费的食物折合成粮食大约是210 000 000人一年的口粮，将210 000 000用科学记数法表示为（）

A、2.1 $\times$ 10 ⁸ B、0.21 $\times$ 10 ⁹ C、2.1 $\times$ 10 ⁹ D、21 $\times$ 10 ⁷

查看试题解析
3. 如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（）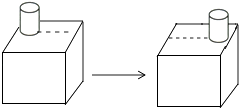

A、主视图 B、左视图 C、俯视图 D、主视图和俯视图

查看试题解析
4. 不等式组 ${\begin{matrix} 3 - 2 x < 5 \\ 2 (x - 2) \leq 1 \end{matrix}$ 的解集是（）

A、无解 B、 $x < - 1$ C、x ≥ $\frac{5}{2}$ D、－1<x ≤ $\frac{5}{2}$

查看试题解析
5. 如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为（）

A、4 B、4 $\sqrt{2}$ C、6 D、4 $\sqrt{3}$

查看试题解析
6. 学校团委组织“阳光助残”捐款活动，九年级一班学生捐款情况如下表：
捐款金额/元
5
10
20
50
人数/人
10
13
12
15
则学生捐款金额的中位数是（）

A、13元 B、12元 C、10元 D、20元

查看试题解析
7.
如图，直线a与直线b交于点A，与直线c交于点B，∠1=120°，∠2=45°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转（　　）

A、15° B、30° C、45° D、60°

查看试题解析
8. 从甲、乙、丙、丁4名三好学生中随机抽取2名学生担任升旗手，则抽取的2名学生是甲和乙的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
9. 如图所示，△ABC中，∠ABC ＝∠BAC，D是AB的中点，EC∥AB，DE∥BC，AC与DE相交于O，下列结论中，不一定成立的是（）

A、AD＝EC B、AC＝DE C、AB＝AC D、OA＝OE

查看试题解析
10. 二次函数y＝－x²＋bx＋c的图象如图所示，下列几个结论：
①对称轴为直线x＝2；
②当y≤0时，x < 0或x > 4；
③函数解析式为y＝－x²＋4x；
④当x≤0时，y随x的增大而增大．其中正确的结论有（）

A、①②③④ B、①②③ C、②③④ D、①③④

查看试题解析

二、填空题

11. 计算：2018⁰－ $| - 2 |$ ＝．

查看试题解析
12. 关于x的一元二次方程x²－ $\sqrt{2}$ x＋sinα＝0有两个相等的实数根，则锐角α＝．

查看试题解析
13. 如图，菱形AOCB的顶点A坐标为（3，4），双曲线y＝ $\frac{k}{x}$ （x >0）的图象经过点B，则k的值为.

查看试题解析
14. 如图，在Rt△ABC中，∠ACB ＝90°，AC ＝BC ＝2，以点A为圆心，AC的长为半径作弧CE交AB于点E，以点B为圆心，BC的长为半径作弧CD交AB于点D．则阴影部分的面积为．

查看试题解析
15. 如图，Rt△ABC中，∠ACB ＝ 90°，AC ＝3，AB ＝5，D是BC上一动点（D与B、C不重合），连接AD，将△ACD沿AD折叠，点C落在点E处，连接DE交AB于点F，当△DEB是直角三角形时，DF的长为.

查看试题解析

三、解答题

16. 化简 $\frac{a}{a^{2} - 4} \div \frac{a^{2} - 3 a}{a + 2} - \frac{1}{2 - a}$ ，并求值，其中a与2，3构成△ABC的三边，且a为整数．

查看试题解析
17. 如图，AB为⊙O的直径，点D，E是位于AB两侧的半圆AB上的动点，射线DC切⊙O于点D．连接DE，AE，DE与AB交于点P，F是射线DC上一动点，连接FP，FB，且∠AED＝45°．

(1)、求证：CD∥AB；

(2)、填空：
①若DF＝AP，当∠DAE＝时，四边形ADFP是菱形；
②若BF⊥DF，当∠DAE＝时，四边形BFDP是正方形．

查看试题解析
18. 为了丰富同学的课余生活，某学校将举行“亲近大自然”户外活动，现随机抽取了部分学生进行主题为“你最想去的景点是 ”的问卷调查，要求学生只能从“A（绿博园），B（人民公园），C（湿地公园），D（森林公园）”四个景点中选择一项，根据调查结果，绘制了如下两幅不完整的统计图．

回答下列问题：

(1)、本次共调查了多少名学生？

(2)、补全条形统计图；

(3)、若该学校共有3 600名学生，试估计该校去湿地公园的学生人数．

查看试题解析
19. 如图，在平面直角坐标系中，一次函数y = m x＋n（m≠0）的图象与反比例函数y= $\frac{k}{x}$ (k ≠0）的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为M，BM=OM，OB=2 $\sqrt{2}$ ，点A的纵坐标为4．

(1)、求该反比例函数和一次函数的解析式；

(2)、连接MC，求四边形MBOC的面积．

查看试题解析
20. 为了对一棵倾斜的古杉树AB进行保护，需测量其长度，如图，在地面上选取一点C，测得∠ACB＝45 $°$ ，AC＝24 m，∠BAC＝66.5 $°$ ，求这棵古杉树AB的长度．（结果精确到0.1 m．参考数据：sin66.5 $°$ ≈0.92，cos66.5 $°$ ≈0.40，tan66.5 $°$ ≈2.30）

查看试题解析
21. 某商店欲购进一批跳绳，若同时购进A种跳绳10根和B种跳绳7根，则共需395元，若同时购进A种跳绳5根和B种跳绳3根，共需185元

(1)、求A、B两种跳绳的单价各是多少？

(2)、若该商店准备同时购进这两种跳绳共100根，且A种跳绳的数量不少于跳绳总数量的 $\frac{2}{5}$ ．若每根A种跳绳的售价为26元，每根B种跳绳的售价为30元，问：该商店应如何进货才可获取最大利润，并求出最大利润．

查看试题解析
22. 综合题

(1)、【问题发现】如图（1）四边形ABCD中，若AB=AD，CB=CD，则线段BD，AC的位置关系为；

(2)、【拓展探究】
如图（2）在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；

(3)、【解决问题】如图（3）在正方形ABCD中，AB=2 ，以点A为旋转中心将正方形ABCD旋转60°，
得到正方形AB＇C＇D＇，请直接写出BD＇平方的值．

查看试题解析
23. 已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x²+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．

(1)、求这条抛物线的表达式和点B的坐标；

(2)、点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；

(3)、将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．

查看试题解析

捐款金额/元	5	10	20	50
人数/人	10	13	12	15