河南省濮阳市2018届数学中考一模试卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的相反数是（）

A、 -3 B、3 C、-13 D、13

查看试题解析
2. 今年3月5日，十三届全国人大一次会议在人民大会堂开幕，会议听取了国务院总理李克强关于政府工作的报告. 其中表示，五年来，人民生活持续改善，脱贫攻坚取得决定性进展，贫困人口减少6800多万，易地扶贫搬迁830万人，贫困发生率由10.2%下降到3.1%.将830万用科学记学法表示为（）

A、 $83 \times 10^{5}$ B、 $0.83 \times 10^{6}$ C、 $8.3 \times 10^{6}$ D、 $8.3 \times 10^{7}$

查看试题解析
3. 如图是由三个小正方体叠成的一个几何体，它的左视图是（）．

A、 B、 C、 D、

查看试题解析
4. 下列各式计算正确的是（）

A、2ab+3ab=5ab B、 ${(- a^{2} b^{3})}^{2} = a^{4} b^{5}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ D、 ${(a + 1)}^{2} = a^{2} + 1$

查看试题解析
5. 不等式组 ${\begin{matrix} 2 - x \geq 1 \\ 2 x - 1 > - 7 \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
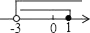6. 如图，直线AB与直线CD相交于点O，E是∠COB内一点，且OE⊥AB，∠AOC=35°，则∠EOD的度数是（）

A、155° B、145° C、135° D、125°

查看试题解析
7. 在学校举行“阳光少年，励志青春”的演讲比赛中，五位评委给选手小明的平分分别为：90，85，90，80，95，则这组数据的众数是（）

A、95 B、90 C、85 D、80

查看试题解析
8. 某校组织九年级学生参加中考体育测试，共租3辆客车，分别标号1，2，3，李军和赵娟两人可以任选一辆车坐，则两人同坐2号车的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图，在平面直角坐标系中，Rt△ABC的斜边BC在x轴上，点B坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后向下平移2个单位，则A点的对应点的坐标为（）

A、 $(- 2 ， - 2 + \sqrt{3})$ B、 $(- 2 ， - 2 - \sqrt{3})$ C、 $(- 4 ， - 2 - \sqrt{3})$ D、 $(- 4 ， - 2 + \sqrt{3})$

查看试题解析
10. 若关于x的方程 $x^{2} + x - a + \frac{5}{4} = 0$ 有两个不相等的实数根，则满足条件的最小整数a的值是（）

A、-1 B、0 C、1 D、2

查看试题解析

二、填空题

11. 计算： $2 sin 30 ° + {(- 1)}^{- 2} - | 2 - \sqrt{2} | =$ .

查看试题解析
12. 若二次函数 $y = a x^{2} + b x + c (a < 0)$ 的图像经过（2，0），且其对称轴为直线x=-1，则当函数值y>0成立时，x的取值范围是.

查看试题解析
13. 如图，已知双曲线 $y = \frac{k}{x}$ (k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为．

查看试题解析
14. 如图，将矩形ABCD绕点C沿顺时针方向旋转90°到矩形 $A' B' C' D'$ 的位置，AB=2，
AD=4，则阴影部分的面积为.

查看试题解析
15. 如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，点D，E为AC，BC上两个动点，若将∠C沿DE折叠，点C的对应点 $C'$ 恰好落在AB上，且 $Δ A D C'$ 恰为直角三角形，则此时CD的长为.

查看试题解析

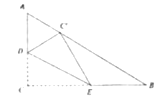
三、解答题

16. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div (1 + \frac{2}{a - 1})$ ，其中 $a = \sqrt{2} + 1$

查看试题解析
17. 某校在3月份举行读书节活动，鼓励学生进行有益的课外阅读，张老师为了了解该校学生课外阅读的情况，设计了“你最喜欢的课外读物类型”的调查问卷，包括“名著”“科幻”“历史”“童话”四类，在学校随机抽取了部分学生进行调查，被抽取的学生只能在四种类型中选择其中一类，最后将调查结果绘制成如下两幅尚不完整的统计图.

请你根据以上信息解答下列问题：

(1)、本次调查中，张老师一共调查了名学生；

(2)、求本次调查中选择“历史”类的女生人数和“童话”类的男生人数，并将条形统计图补充完整；

(3)、扇形图中“童话”类对应的圆心角度数为.

(4)、如果该校共有学生360名，请估算该校最喜欢“名著”类和“历史”类的学生总人数.

查看试题解析
18. 如图，已知△ABC内接于 $⊙ O$ ，AB是直径，OD∥AC，AD=OC.

(1)、求证：四边形OCAD是平行四边形；

(2)、填空：①当∠B=时，四边形OCAD是菱形；
②当∠B=时，AD与 $⊙ O$ 相切.

查看试题解析
19. 如图，线段AB、CD分别表示甲乙两建筑物的高，BA⊥AD，CD⊥DA，垂足分别为A、D．从D点测到B点的仰角α为60°，从C点测得B点的仰角β为30°，甲建筑物的高AB=30米

(1)、求甲、乙两建筑物之间的距离AD．

(2)、求乙建筑物的高CD．

查看试题解析
20. 如图，一次函数y=kx+b的图象与反比例函数y= $\frac{m}{x}$ 的图象交于点A（﹣3，m+8），B（n，﹣6）两点．

(1)、求一次函数与反比例函数的解析式；

(2)、求△AOB的面积．

查看试题解析
21. 每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购. 经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元.

(1)、求甲、乙两种型号设备的价格；

(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；

(3)、在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.

查看试题解析
22. 如图1，在四边形ABCD中，AB=AD. ∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF= $\frac{1}{2}$ ∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系.

(1)、思路梳理
将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合.由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线. 易证△AFG $≅$ ，故EF，BE，DF之间的数量关系为；

(2)、类比引申
如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC的延长线上，∠EAF= $\frac{1}{2}$ ∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明.

(3)、联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°. 若BD=1，EC=2，则DE的长为.

查看试题解析
23. 如图，抛物线 y=ax²+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC=3OB．

(1)、求抛物线的解析式，并写出x为何值y = 0；

(2)、点D在y轴上，且∠BDO=∠BAC，求点D的坐标；

(3)、点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N 为顶点的四边形是平行四边形？若存在，求出所有符合条件的点 M 的坐标；若不存在，请说明理由．

查看试题解析