甘肃省2018届数学普通高中招生模拟考试试卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 宁波栎社国际机场三期扩建工程建设总投资84.5亿元，其中84.5亿元用科学记数法表示为（）

A、0.845×10¹⁰元 B、84.5×10⁸元 C、8.45×10⁹元 D、8.45×10¹⁰元

查看试题解析
3. 64的立方根是（）

A、4 B、8 C、±4 D、±8

查看试题解析
4. 下列计算正确的是（）

A、2x²·2xy＝4x³y⁴ B、3x²y－5xy²＝－2x²y C、x^－¹÷x^－²＝x^－¹ D、(－3a－2)(－3a＋2)＝9a²－4

查看试题解析
5. 如图，一个正方体切去一个三棱锥后所得几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在△ABC中，AB＝AC，BC＝6，△DEF的周长是7，AF⊥BC于点F，BE⊥AC于点E，且点D是AB的中点，则AF的长为（）

A、 $\sqrt{5}$ B、 $\sqrt{7}$ C、 $\sqrt{3}$ D、7

查看试题解析
7. 在同一平面坐标系内，若直线y＝3x－1与直线y＝x－k的交点在第四象限的角平分线上，则k的值为（）

A、k＝－ $\frac{1}{2}$ B、k＝ $\frac{1}{3}$ C、k＝ $\frac{1}{2}$ D、k＝1

查看试题解析
8. 若x₁ ， x₂是一元二次方程x²﹣2x﹣1=0的两个根，则x₁²﹣x₁+x₂的值为（）

A、﹣1 B、0 C、2 D、3

查看试题解析
9. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（）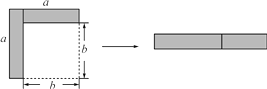

A、(a－b)²＝a²－2ab＋b² B、a(a－b)＝a²－ab C、(a－b)²＝a²－b² D、a²－b²＝(a＋b)(a－b)

查看试题解析
10. 如图，直线l的解析式为y=﹣x+4，它与x轴和y轴分别相交于A，B两点．平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动．它与x轴和y轴分别相交于C，D两点，运动时间为t秒（0≤t≤4），以CD为斜边作等腰直角三角形CDE（E，O两点分别在CD两侧）．若△CDE和△OAB的重合部分的面积为S，则S与t之间的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 因式分解：b²－ab＋a－b＝．

查看试题解析
12. 方程 $\frac{1}{2 x}$ ＝ $\frac{2}{x - 3}$ 的解是．

查看试题解析
13. 若单项式﹣x^m^﹣²y³与 $\frac{2}{3}$ xⁿy^2m^﹣³ⁿ的和仍是单项式，则m^﹣ⁿ= ．

查看试题解析
14. 如图，OP平分∠AOB，∠AOP=15°，PC∥OB，PD⊥OB于点D，PD=4，则PC等于．

查看试题解析
15. 若a、b、c为三角形的三边，且a、b满足 $\sqrt{a - 9} + {(b - 2)}^{2} = 0$ ，第三边c为奇数，则c= ．

查看试题解析
16. 若关于x的一元二次方程（k﹣1）x²﹣4x﹣5=0没有实数根，则k的取值范围是．

查看试题解析
17. 如图，已知AB是⊙O的弦，半径OC垂直AB，点D是⊙O上一点，且点D与点C位于弦AB两侧，连接AD、CD、OB，若∠BOC=70°，则∠ADC=度．

查看试题解析
18. 已知a₁＝－ $\frac{3}{2}$ ，a₂＝ $\frac{5}{5}$ ，a₃＝－ $\frac{7}{10}$ ，a₄＝ $\frac{9}{17}$ ，a₅＝－ $\frac{11}{26}$ ，…，则a₈＝．

查看试题解析

三、解答题

19. 计算

(1)、计算：( $\frac{1}{3}$ )^－²－(π－ $\sqrt{7}$ )⁰＋| $\sqrt{3}$ －2|＋6tan30°；

(2)、先化简，再求值：( $\frac{3 x}{x - 2}$ － $\frac{x}{x + 2}$ )÷ $\frac{x}{x^{2} - 4}$ ，其中x＝－1.

查看试题解析
20. 已知关于x的不等式 $\frac{2 m - m x}{2} > \frac{1}{2} x - 1$ ．

(1)、当m=1时，求该不等式的解集；

(2)、m取何值时，该不等式有解，并求出解集．

查看试题解析
21. 如图，利用尺规，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）

查看试题解析
22. 如图，在▱ABCD中，DE＝CE，连接AE并延长交BC的延长线于点F.

(1)、求证：△ADE≌△FCE；

(2)、若AB＝2BC，∠F＝36°，求∠B的度数．

查看试题解析
23. 在一次数学兴趣小组活动中，李燕和刘凯两位同学设计了如图所示的两个转盘做游戏（每个转盘被分成面积相等的几个扇形，并在每个扇形区域内标上数字）．游戏规则如下：两人分别同时转动甲、乙转盘，转盘停止后，若指针所指区域内两数和小于12，则李燕获胜；若指针所指区域内两数和等于12，则为平局；若指针所指区域内两数和大于12，则刘凯获胜（若指针停在等分线上，重转一次，直到指针指向某一份内为止）．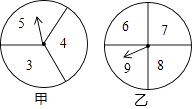

(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果；

(2)、分别求出李燕和刘凯获胜的概率．

查看试题解析
24. 某校为了进一步改进本校七年级数学教学，提高学生学习数学的兴趣，校教务处在七年级所有班级中，每班随机抽取了6名学生，并对他们的数学学习情况进行了问卷调查．我们从所调查的题目中，特别把学生对数学学习喜欢程度的回答（喜欢程度分为：“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”，针对这个题目，问卷时要求每位被调查的学生必须从中选一项且只能选一项）结果进行了统计，现将统计结果绘制成如下两幅不完整的统计图．
请你根据以上提供的信息，解答下列问题：

(1)、补全上面的条形统计图和扇形统计图；

(2)、所抽取学生对数学学习喜欢程度的众数是；

(3)、若该校七年级共有960名学生，请你估算该年级学生中对数学学习“不太喜欢”的有多少人？

查看试题解析
25. 如图，在平面直角坐标系中，一次函数y＝ax＋b(a≠0)的图象与反比例函数y＝ $\frac{k}{x}$ (k≠0)的图象交于A，B两点，与x轴交于点C，过点A作AH⊥x轴于点H，点O是线段CH的中点，AC＝4 $\sqrt{5}$ ，cos∠ACH＝ $\frac{\sqrt{5}}{5}$ ，点B的坐标为(4，n)．

(1)、求该反比例函数和一次函数的解析式；

(2)、求△BCH的面积．

查看试题解析
26. 如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．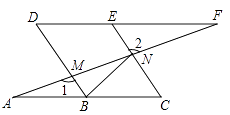

(1)、求证：四边形BCED是平行四边形；

(2)、已知DE=2，连接BN，若BN平分∠DBC，求CN的长．

查看试题解析
27. 如图，在等腰△ABC中，AB=BC，以BC为直径的⊙O与AC相交于点D，过点D作DE⊥AB交CB延长线于点E，垂足为点F．

(1)、判断DE与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径R=5，tanC= $\frac{1}{2}$ ，求EF的长．

查看试题解析
28. 如图甲，直线y=﹣x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x²+bx+c与x轴的另一个交点为A，顶点为P．

(1)、求该抛物线的解析式；

(2)、在该抛物线的对称轴上是否存在点M，使以C，P，M为顶点的三角形为等腰三角形？若存在，请直接写出所符合条件的点M的坐标；若不存在，请说明理由；

(3)、当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值（图乙、丙供画图探究）．

查看试题解析