安徽省安顺2018届数学中考模拟试卷

试卷更新日期：2018-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 2018相反数的倒数是（）

A、 2018 B、﹣2018 C、︱-2018︱ D、﹣ $\frac{1}{2018}$

查看试题解析
2. 下面四个图形分别是节能、节水、绿色食品和低碳标志，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、a⁵＋a²＝a⁷ B、 $\sqrt{2}$ × $\sqrt{3}$ ＝ $\sqrt{6}$ C、2-2＝－4 D、x²·x³＝x⁶

查看试题解析
4. 如图，直线AB、CD相交于点O，∠BOE=90°，OF平分∠AOE，∠1=15°30’，则下列结论不正确的是（）

A、∠2=45° B、∠1=∠3 C、∠AOD+∠1=180° D、∠EOD=75°30＇

查看试题解析
5. 由若干个小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体所用的小正方体的个数最少是（）

A、7 B、8 C、9 D、10

查看试题解析
6. 如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
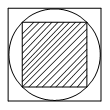7. 近年来，我国持续大面积的雾霾天气让环保和健康问题成为焦点，为进一步普及环保和健康知识，我市某校举行了“建设宜居成都，关注环境保护”的知识竞赛，某班学生的成绩统计如下：
成绩（分）
60
70
80
90
100
人数
4
8
12
11
5
则该班学生成绩的众数和中位数分别是（）

A、70分，80分 B、80分，80分 C、90分，80分 D、80分，90分

查看试题解析
8. 设n为正整数，且n＜ $\sqrt{65}$ ＜n+1，则n的值为（　　）

A、5 B、6 C、7 D、8

查看试题解析
9. 如图所示，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接正方形的面积为（）

A、2 B、4 C、8 D、16

查看试题解析
10. 如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH=DF，连接AH、FH，FH与AC交于点M，以下结论：
①FH=2BH；②AC⊥FH；③S_△_ACF=1；④CE= $\frac{1}{2}$ AF；⑤ $E G^{2}$ =FG•DG，其中正确结论的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
11. 将抛物线y=x²﹣1向下平移8个单位长度后与x轴的两个交点之间的距离为（）

A、4 B、6 C、8 D、10

查看试题解析
12. 如图所示，在平面直角坐标系中，矩形ABCD的BC边落在y轴上，其它部分均在第一象限，双曲线y= $\frac{k}{x}$ 过点A，延长对角线CA交x轴于点E，以AD、AE为边作平行四边形AEFD，若平行四边形AEFD的面积为4，则k值为（）

A、2 B、4 C、8 D、12

查看试题解析

二、填空题

13. 分解因式：12x²﹣3y²= ．

查看试题解析
14. 在函数y= $\sqrt{x - 1}$ + $\sqrt{2 - x}$ 中，自变量x的取值范围是.

查看试题解析
15. 自中国提出“一带一路·合作共赢”的倡议以来，一大批中外合作项目稳步推进.其中，由中国承建的蒙内铁路（连接肯尼亚首都罗毕和东非第一大港蒙巴萨港），是首条海外中国标准铁路，已于2017年5月31日正式投入运营.该铁路设计运力为25000000吨，将25000000吨用科学记数法表示，记作吨.

查看试题解析
16. 已知关于x的一元二次方程（m-2）x²+2x+1=0有实数根，则m的取值范围是．

查看试题解析
17. 如图，AD和CB相交于点E，BE=DE，请添加一个条件，使△ABE≌△CDE（只添一个即可），你所添加的条件是．

查看试题解析
18. 某市今年起调整居民用水价格，每立方米水费上涨20%，小方家去年12月份的水费是26元，而今年5月份的水费是50元．已知小方家今年5月份的用水量比去年12月份多8立方米，设去年居民用水价格为x元/立方米，则所列方程为．

查看试题解析

三、解答题

19. 计算： 2cos²45°－ $\sqrt{（ tan 60^{0} - 2)^{2}}$ －(sin60°－1)⁰＋( $\frac{1}{2}$ )^－2.

查看试题解析
20. 先化简，再求值：
（ $\frac{x^{2}}{x^{2} + x}$ ﹣1）÷ $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，其中x的值从不等式组 ${\begin{matrix} - x \leq 1 \\ 2 x - 1 < 4 \end{matrix}$ 的整数解中故答案为：取．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数y＝ax＋b(a≠0)的图象与反比例函数y＝ $\frac{k}{x}$ (k≠0)的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH＝3，tan∠AOH＝ $\frac{4}{3}$ ，点B的坐标为(m，－2)．

(1)、求△AHO的周长；

(2)、求该反比例函数和一次函数的解析式．

查看试题解析
22. 如图，AB为⊙O的直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，过点C作CE⊥DB交DB的延长线于点E，直线AB与CE相交于点F．

(1)、求证：CF为⊙O的切线；

(2)、填空：当∠CAB的度数为时，四边形ACFD是菱形．

查看试题解析
23. 经市场调查，某种商品在第x天的售价与销量的相关信息如下表；已知该商品的进价为每件30元，设销售该商品每天的利润为y元．
时间x（天）
1≤x≤50
50≤x≤90
售价（元/件）
x+40
90
每天销量（件）
200-2x

(1)、求出y与x的函数关系式

(2)、问销售该商品第几天时，当天销售利润最大？最大利润是多少？

(3)、该商品销售过程中，共有多少天日销售利润不低于4800元？直接写出答案．

查看试题解析
24. 某校兴趣小组想测量一座大楼AB的高度．如图6，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i=1： $\sqrt{3}$ ．在离C点40米的D处，用测角仪测得大楼顶端A的仰角为37°，测角仪DE的高为1.5米，求大楼AB的高度约为多少米？（结果精确到0.1米）
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{3}$ ≈1.73．）

查看试题解析
25. 为迎接安顺市文明城市创建工作，某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动，成绩分为A、B、C、D四个等级，并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息，解答下列各题：

(1)、求八年一班共有多少人；

(2)、补全折线统计图；

(3)、在扇形统计图中等极为“D”的部分所占圆心角的度数为；

(4)、若等级A为优秀，求该班的优秀率.

查看试题解析
26. 已知抛物线y=ax²+bx+c经过A（﹣1，0），B（3，0），C（0，3）三点，直线L是抛物线的对称轴．

(1)、求抛物线的函数关系式；

(2)、求抛物线的顶点坐标；

(3)、设P点是直线L上的一个动点，当△PAC的周长最小时，求点P的坐标．

查看试题解析

时间x（天）	1≤x≤50	50≤x≤90
售价（元/件）	x+40	90
每天销量（件）	200-2x

成绩（分）	60	70	80	90	100
人数	4	8	12	11	5