2018年高考数学提分专练：第13题 立体几何（填空题）
试卷更新日期：2018-05-16 类型：二轮复习
一、真题演练
-
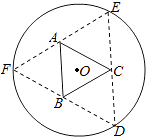
1. 已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径，若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为 ．2.
如图，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O．D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为 ．
3. 长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为 ．4. a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60°角时，AB与b成30°角；
②当直线AB与a成60°角时，AB与b成60°角；
③直线AB与a所成角的最小值为45°；
④直线AB与a所成角的最小值为60°；
其中正确的是（填写所有正确结论的编号）
二、模拟实训
-
5. 某几何体的三视图如图，则该几何体的体积为 ．
6. 如图所示（单位：cm），图中阴影部分绕AB旋转一周所形成的几何体的体积为 ．
7. 已知 是球 表面上的点， 平面 ， ， ， ，则球 的表面积为 ．8. 已知三棱锥 ， 面 ， 中两直角边 ， ，该三棱锥的外接球的表面积为 ，则三棱锥的体积为 ．
9. 如图，三棱锥的所有顶点都在一个球面上，在△ABC中，AB= ，∠ACB=60°，∠BCD=90°，AB⊥CD ， CD= ，则该球的体积为 ．
10. 下列四个结论中假命题的序号是 ．①垂直于同一直线的两条直线互相平行；
②平行于同一直线的两直线平行；
③若直线a，b，c满足a∥b，b⊥c，则a⊥c；
④若直线a，b是异面直线，则与a，b都相交的两条直线是异面直线．
11. 已知关于空间两条不同直线m，n，两个不同平面α，β，有下列四个命题：①若m∥α且n∥α，则m∥n；②若m⊥β且m⊥n，则n∥β；③若m⊥α且m∥β，则α⊥β；④若n⊂α且m不垂直于α，则m不垂直于n．其中正确命题的序号为 ．12. 如图，在直三棱柱ABC﹣A1B1C1中，AB=1，BC=2，BB1=3，∠ABC=90°，点D为侧棱BB1上的动点，当AD+DC1最小时，三棱锥D﹣ABC1的体积为 ．
13. 已知边长为 的正△ABC的三个顶点都在球O的表面上，且OA与平面ABC所成的角为60° ， 则球O的表面积为 ．14. 如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD，现将四边形ABCD沿BD折成直二面角A﹣BD﹣C，则三棱锥A﹣BCD的外接球的体积为cm3 ．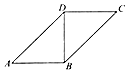
15. 某几何体的三视图如图所示，该几何体的体积为 ．
16. 某三棱锥的三视图是三个边长相等的正方形及对角线，若该三棱锥的体积是 ，则它的表面积是 ．
17. 半径为R的球放在房屋的墙角处，球与围成墙角的三个互相垂直的面都相切，若球心到墙角的距离是 ，则球的表面积是 ．
