2016-2017学年天津市西青区杨柳青三中九年级上学期期中数学试卷

试卷更新日期：2016-12-21 类型：期中考试

进入出卷网下载

一、选择题

1. 下列电视台的台标，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在直角坐标系中，点A（2，﹣3）关于原点对称的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列方程是关于x的一元二次方程的是（）

A、ax²+bx+c=0 B、 $\frac{1}{x^{2}} + \frac{1}{x}$ =2 C、x²+2x=x²﹣1 D、3（x+1）²=2（x+1）

查看试题解析
4. 下列函数中，不是二次函数的是（　　）

A、y=1﹣ $\sqrt{2}$ x² B、y=2（x﹣1）²+4 C、y= $\frac{1}{2}$ （x﹣1）（x+4） D、y=（x﹣2）²﹣x²

查看试题解析
5. 如图，△ABC和△DCE都是直角三角形，其中一个三角形是由另一个三角形旋转得到的，下列叙述中错误的是（）

A、旋转中心是点C B、顺时针旋转角是90° C、旋转中心是点B，旋转角是∠ABC D、既可以是逆时针旋转又可以是顺时针旋转

查看试题解析
6. 如图，CE是圆O的直径，⊙O的直径，AB为⊙O的弦，EC⊥AB，垂足为D，下面结论正确的有（）
①AD=BD；② $\hat{A C}$ = $\hat{B C}$ ；③ $\hat{A E}$ = $\hat{B E}$ ；④OD=CD．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知：如图，⊙O的两条弦AE，BC相交于点D，连接AC，BE．若∠ACB=60°，则下列结论中正确的是（）

A、∠AOB=60° B、∠ADB=60° C、∠AEB=60° D、∠AEB=30°

查看试题解析
8. 一元二次方程x²﹣mx+2m=0有两个相等的实数根，则m等于（）

A、0或8 B、0 C、8 D、2

查看试题解析
9. 如图，抛物线顶点坐标是P（1，3），则函数y随自变量x的增大而减小的x的取值范围是（）

A、x＞3 B、x＜3 C、x＞1 D、x＜1

查看试题解析
10. 如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A=22.5°，OC=4，CD的长为（）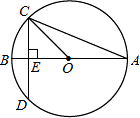

A、2 $\sqrt{2}$ B、4 C、4 $\sqrt{2}$ D、8

查看试题解析
11. 二次函数y=ax²+bx+c的图象如图，点（1，0）在函数图象上，那么abc、2a+b、a+b+c、a﹣b+c这四个代数式中，值大于或等于零的数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图所示，MN是⊙O的直径，作AB⊥MN，垂足为点D，连接AM，AN，点C为 $\hat{A N}$ 上一点，且 $\hat{A C}$ = $\hat{A M}$ ，连接CM，交AB于点E，交AN于点F，现给出以下结论：
①AD=BD；②∠MAN=90°；③ $\hat{A M}$ = $\hat{B M}$ ；④∠ACM+∠ANM=∠MOB；⑤AE= $\frac{1}{2}$ MF．
其中正确结论的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 已知x₁ ， x₂是方程2x²﹣5x﹣1=0的两个根，则x₁+x₂的值是．

查看试题解析
14. 如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=6，AB=10，OD⊥BC于点D，则OD的长为．

查看试题解析
15. 圆的两条平行弦的长分别为6、8，若圆的半径为5，则这两条平行弦之间的距离为．

查看试题解析
16. 如果将抛物线y=x²+2x﹣1向上平移，使它经过点A（0，3），那么所得新抛物线的表达式是．

查看试题解析
17. 如图，Rt△ABC中，∠ABC=90°，AB=BC=2，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，那么BM的长是．

查看试题解析
18. 若二次函数y=ax²+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x₁ ， 0）、（x₂ ， 0），且x₁＜x₂ ，图象上有一点M（x₀ ， y₀）在x轴下方，在下列四个算式中判定正确的是
①a（x₀﹣x₁）（x₀﹣x₂）＜0；②a＞0；③b²﹣4ac≥0；④x₁＜x₀＜x₂ ．

查看试题解析

三、解答题

19. 已知：关于x的方程x²+2mx+m²﹣1=0

(1)、不解方程，判别方程根的情况；

(2)、若方程有一个根为3，求m的值．

查看试题解析
20. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点三角形ABC（顶点时网格线的交点）

(1)、将△ABC绕C点顺时针旋转90°，得到△A₁B₁C，请画出△A₁B₁C；

(2)、求线段BB₁的长度为．

查看试题解析
21. 抛物线y=﹣ $\frac{1}{2}$ x²+bx+c与x轴分别交于点A（﹣2，0）、B（4，0），与y轴交于点C．

(1)、求抛物线解析式；

(2)、求△CAB的面积．

查看试题解析
22. 如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC．

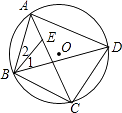(1)、若∠CBD=39°，求∠BAD的度数；

(2)、求证：∠1=∠2．

查看试题解析
23. 某商品现在的售价为每件30元，每天可卖出40件．市场调查反映：如果调整价格，每降价1元，每天可多卖出2件．请你帮助分析，当每件商品降价多少元时，可使每天的销售额最大，最大销售额是多少？设每件商品降价x元，每天的销售额为y元．

(1)、分析：根据问题中的数量关系，用含x的式子填表：
原价
每件降价1元
每件降价2元
…
每件降价x元
每件售价（元）
30
29
28
…
每天销量（件）
40
42
44
…

(2)、由以上分析，用含x的式子表示y，并求出问题的解．

查看试题解析
24.
如图1，将两个完全相同的三角形纸片ABC和A′B′C重合放置，其中∠C=90°，∠B=∠B′=30°，AC=AC′=2．

(1)、如图2，固定△ABC，将△A′B′C绕点C旋转，当点A′恰好落在AB边上时，
①∠CA′B′=；旋转角ɑ=（0°＜ɑ＜90°），线段A′B′与AC的位置关系是；

(2)、
②设△A′BC的面积为S₁ ， △AB′C的面积为S₂ ，则S₁与S₂的数量关系是什么？证明你的结论；

(3)、
如图3，∠MON=60°，OP平分∠MON，OP=PN=4，PQ∥MO交ON于点Q．若在射线OM上存在点F，使S_△_PNF=S_△_OPQ ，请直接写出相应的OF的长．

查看试题解析
25. 已知抛物线的不等式为y=﹣x²+6x+c．

(1)、若抛物线与x轴有交点，求c的取值范围；

(2)、设抛物线与x轴两个交点的横坐标分别为x₁ ， x₂ ．若x₁²+x₂²=26，求c的值．

(3)、
若P，Q是抛物线上位于第一象限的不同两点，PA，QB都垂直于x轴，垂足分别为A，B，且△OPA与△OQB全等．求证：c＞﹣ $\frac{21}{4}$ ．

查看试题解析

	原价	每件降价1元	每件降价2元	…	每件降价x元
每件售价（元）	30	29	28	…
每天销量（件）	40	42	44	…